Advertisements
Advertisements
Question
The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
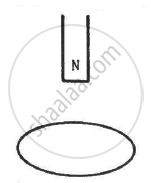
Solution
Given:-
Initial flux, ϕ1 = 0.35 weber
Final flux ϕ2 = 0.85 weber
∴ Δϕ = ϕ2 − ϕ1
= (0.85 − 0.35) weber
= 0.5 weber
Also,
Δt = 0.5 s
The magnitude of the induced emf is given by
\[e = \frac{∆ \phi}{∆ t} = \frac{0 . 5}{0 . 5} = 1 V\]
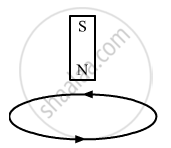
The induced current is anti-clockwise when seen from the side of the magnet.
APPEARS IN
RELATED QUESTIONS
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
Figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mΩ. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s−1 in the direction shown. Give the polarity and magnitude of the induced emf.
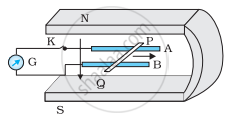
(b) Is there an excess charge built up at the ends of the rods when K is open? What if K is closed?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed = (12 cm s−1) when K is closed? How much power is required when K is open?
(f) How much power is dissipated as heat in the closed circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

What is motional emf? State any two factors on which it depends.
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
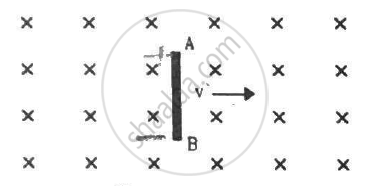
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
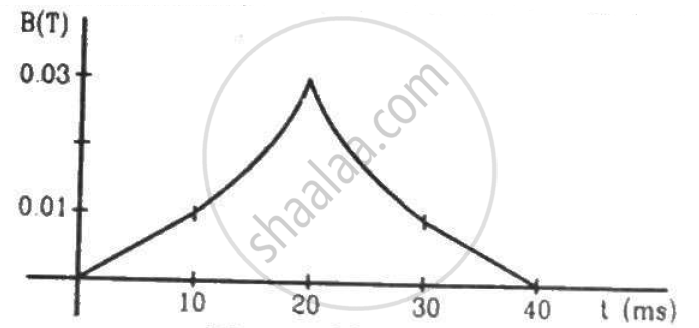
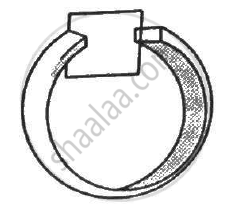
Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h−1? The vertical component of earth's magnetic field is 0.2 × 10−4 T and the rails are separated by 1 m.
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
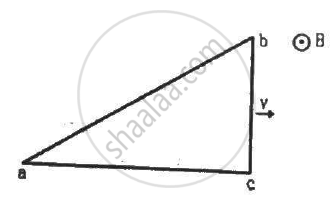
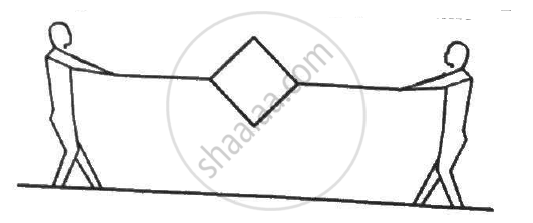
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
Figure shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i = i0 sin ωt. Find (a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to \[\frac{20\pi}{\omega}.\]
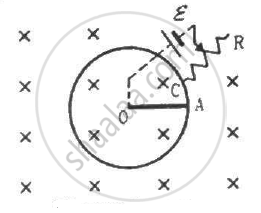
Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. A battery of emf ε and a variable resistance R are connected between O and C. Neglect the resistance of the connecting wires. Let θ be the angle made by the rod from the horizontal position (show in the figure), measured in the clockwise direction. During the part of the motion 0 < θ < π/4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
