Advertisements
Advertisements
Question
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
Solution
The angular velocity of the disc is ω. Also, the magnetic field of magnitude B is perpendicular to the disc.
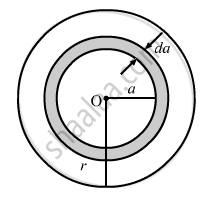
Let us take a circular element of thickness da at a distance a from the centre.
Linear speed of the element at a from the centre, v = ωa
Now,
\[de = Blv\]
\[de = B \times da \times a\omega\]
\[ \Rightarrow e = \int_0^r \left( B\omega a \right)da\]
\[ e = \frac{1}{2}B\omega r^2\]
APPEARS IN
RELATED QUESTIONS
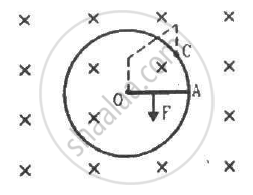
Consider the situation shown in the figure. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance Runiformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠ AOC = 90°.
A cycle wheel of radius 0.6 m is rotated with constant angular velocity of 15 rad/s in a region of magnetic field of 0.2 T which is perpendicular to the plane of the wheel. The e.m.f generated between its center and the rim is, ____________.
A conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular to one of its side. A magnetic induction B constant in time and space, pointing perpendicular and into the plane of the loop exists everywhere. The current induced in the loop is ______.
A straight conductor of length 2 m moves in a uniform magnetic field of induction 2.5 x `10^-3` T with a velocity. of 4 m/s in a direction perpendicular to its length and also perpendicular to the field. The e.m.f. induced between the ends of the conductor is ______.
A wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the e.m.f. induced in the wire is 2 V, the magnitude of the field in tesla is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
A 0.1 m long conductor carrying a current of 50 A is held perpendicular to a magnetic field of 1.25 mT. The mechanical power required to move the conductor with a speed of 1 ms-1 is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
A bicycle generator creates 1.5 V at 15 km/hr. The EMF generated at 10 km/hr is ______.
Motional e.m.f is the induced e.m.f. ______
An e.m.f is produced in a coil, which is not connected to an external voltage source. This can be due to ______.
- the coil being in a time varying magnetic field.
- the coil moving in a time varying magnetic field.
- the coil moving in a constant magnetic field.
- the coil is stationary in external spatially varying magnetic field, which does not change with time.
A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because ______.
- the magnetic field is constant.
- the magnetic field is in the same plane as the circular coil and it may or may not vary.
- the magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.
- there is a constant magnetic field in the perpendicular (to the plane of the coil) direction.
Find the current in the wire for the configuration shown in figure. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper. θ is a fixed angle made by PQ travelling smoothly over two conducting parallel wires separated by a distance d.
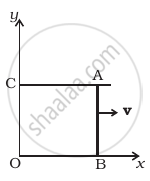
A magnetic field B = Bo sin ( ωt )`hatk` wire AB slides smoothly over two parallel conductors separated by a distance d (Figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?
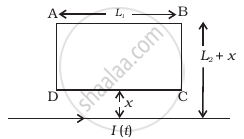
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I(t) = Io (1 – t/T) for 0 ≤ t ≤ T and I(0) = 0 for t > T (Figure). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.
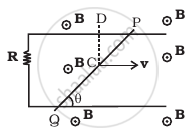
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

A wire 5 m long is supported horizontally at a height of 15 m along an east-west direction. When it is about to hit the ground, calculate the average e.m.f. induced in it. (g = 10 m/s2)
Derive an expression for the total emf induced in a conducting rotating rod.
