Advertisements
Advertisements
Question
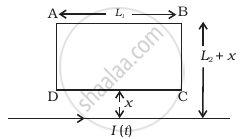
A rectangular loop of wire ABCD is kept close to an infinitely long wire carrying a current I(t) = Io (1 – t/T) for 0 ≤ t ≤ T and I(0) = 0 for t > T (Figure). Find the total charge passing through a given point in the loop, in time T. The resistance of the loop is R.
Solution
To find the charge that passes through the circuit first we have to find the relation between instantaneous current and instantaneous magnetic flux linked with it. The emf induced can be obtained by differentiating the expression of magnetic flux linked w.r.t. t and then applying Ohm’s law, we get
`I = E/R = 1/R (dphi)/(dt)`
According to the problem electric current is given as a function of time.
`I(t) = (dQ)/(dt)` or `(dQ)/(dt) = 1/R (dphi)/(dt)`
Integrating the variable separately in the form of differential equation for finding the charge Q that passed in time t, we have
`Q(t_1) - Q(t_2) = 1/R[phi(t_1) - phi(t_2)]`
For magnetic flux in rectangle:
Magnetic flux due to current carrying conductor at a distance x'
`Q(t) = (mu_0I(t))/(2pix^')`
If length of strip is L1 so total flux on strip of length L1 at distance x' is
`Q(t) = (mu_0I(t))/(2pix^') L_1`
X' varies from x to (x + L2) so total flux in strip
`phi(t) = mu_0/(2pi) L_1 int_x^(x + L_2) (dx)/x^' I(t) = (mu_0L_1)/(2pi) I(t_1) log_e ((L_2 + x))/x`
The magnetic of charge is given on length L1
`int_Q_1 dQ = 1/R int dphi` from (III)
`int_0^Q dQ = 1/R * (mu_0L_1)/(2pi) log_e ((L_2 + x)/x) int_0^1 I(t_1)`
`Q = (mu_0L_1)/(R2pi) log_e ((L_2 + x)/x)(I - 0) = (mu_0L_1I_1)/(2piR) log ((L_2 + x)/x)`
APPEARS IN
RELATED QUESTIONS
An aircraft of wing span of 50 m flies horizontally in the Earth's magnetic field of 6 x 10-5 T at a speed of 400 m/s. Calculate the emf generated between the tips of the wings of the aircraft.
Mechanical force per unit area of a charged conductor is ______
A wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the e.m.f. induced in the wire is 2 V, the magnitude of the field in tesla is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
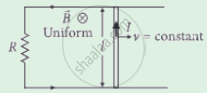
A conducting rod of length l is moving in a transverse magnetic field of strength B with velocity v. The resistance of the rod is R. The current in the rod is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
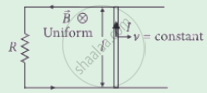
A 0.1 m long conductor carrying a current of 50 A is held perpendicular to a magnetic field of 1.25 mT. The mechanical power required to move the conductor with a speed of 1 ms-1 is ______.
Motional e.m.f is the induced e.m.f. ______
An e.m.f is produced in a coil, which is not connected to an external voltage source. This can be due to ______.
- the coil being in a time varying magnetic field.
- the coil moving in a time varying magnetic field.
- the coil moving in a constant magnetic field.
- the coil is stationary in external spatially varying magnetic field, which does not change with time.
A circular coil expands radially in a region of magnetic field and no electromotive force is produced in the coil. This can be because ______.
- the magnetic field is constant.
- the magnetic field is in the same plane as the circular coil and it may or may not vary.
- the magnetic field has a perpendicular (to the plane of the coil) component whose magnitude is decreasing suitably.
- there is a constant magnetic field in the perpendicular (to the plane of the coil) direction.
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

An aeroplane, with its wings spread 10 m, is flying at a speed of 180 km/h in a horizontal direction. The total intensity of earth's field at that part is 2.5 × 10-4 Wb/m2 and the angle of dip is 60°. The emf induced between the tips of the plane wings will be ______.
