Advertisements
Advertisements
Question
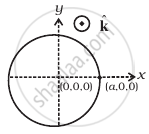
A magnetic field B is confined to a region r ≤ a and points out of the paper (the z-axis), r = 0 being the centre of the circular region. A charged ring (charge = Q) of radius b, b > a and mass m lies in the x-y plane with its centre at the origin. The ring is free to rotate and is at rest. The magnetic field is brought to zero in time ∆t. Find the angular velocity ω of the ring after the field vanishes.
Solution
According to the law of EMI, when magnetic field changes in the circuit, then magnetic flux linked with the circuit also changes and this changing magnetic flux leads to an induced emf in the circuit.
Here, magnetic field decreases which causes induced emf and hence, electric field around the ring. The torque experienced by the ring produces change in angular momentum.
As the magnetic field is brought to zero in time At, the magnetic flux linked with the ring also reduces from maximum to zero. This, in turn, induces an emf in ring as discussed above. The induces emf causes the induced electric field E around the ring.
By the relation between electric field and potential we get,
The induced emf = Electric field E × (2πb) (Because V = E × d) ......(i)
By Faraday's law of EMI
`|ε| = (dphi)/(dt) = A (dB)/(dt)`
`|ε| = (Bpia^2)/(Δt) S` ......(ii)
From equation (i) and (ii), we have
`2pibE = ε = (Bpia^2)/(Δt)`
As we know the electric force experienced by the charged ring, `F_e = QE`. This force try to rotate the coil, and the torque is given by
Torque = b × Force
τ = `QEb = Q[(Bpia^2)/(2piΔt)]b`
⇒ τ = `Q (Ba^2)/(2Δt)`
If ΔL is the change in angular momentum,
ΔL = Torque × Δt = `Q (Ba^2)/2`
Since, initial angular momentum = 0
And Torque × Δt = Change in angular momentum
Final angular momentum = `mb^2ω = (QBa^2)/2`
Where, mb2 = I (moment of inertia of ring)
`ω = (QBa^2)/(2mb^2)`
On rearranging the terms, we have the required expression of angular speed.
APPEARS IN
RELATED QUESTIONS
A jet plane is travelling towards west at a speed of 1800 km/h. What is the voltage difference developed between the ends of the wing having a span of 25 m, if the Earth’s magnetic field at the location has a magnitude of 5 × 10−4 T and the dip angle is 30°.
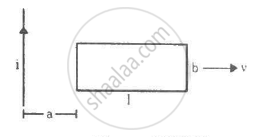
A rectangular metallic loop of length l and width b is placed coplanarly with a long wire carrying a current i (figure). The loop is moved perpendicular to the wire with a speed vin the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of the loop is at a distance a from the wire. solve by using Faraday's law for the flux through the loop and also by replacing different segments with equivalent batteries.
A .0.5m long solenoid of 10 turns/cm has area of cross-section 1cm2 . Calculate the voltage induced across its ends if the current in the solenoid is changed from 1A to 2A in 0.1s.
The two rails of a railway track, insulated from each other and the ground, are connected to millivoltmeter. What is the reading of the millivoltmeter when a train passes at a speed of 180 km/hr along the track, given that the vertical component of earth’s magnetic field is 0.2 × 10–4 wb/m2 and rails are separated by 1 metre ______.
The average e.m.f induced in a coil in which current change from 0.2 ampere to 0.4 ampere in· 0.1 sec is 1 volt, the self-inductance of the coil is
A magnetic field in a certain region is given by `B = B_o cos (ωt)hatk` and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (Figure) . Find the magnitude and the direction of the current at (a, 0, 0) at t = π/2ω, t = π/ω and t = 3π/2ω.
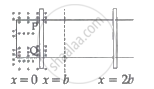
The arm PQ of a rectangular conductor is moving from x = 0 to x = 2b outwards and then inwards from x = 2b to x = 0 as shown in the figure. A uniform magnetic field perpendicular to the plane is acting from x = 0 to x = b. Identify the graph showing the variation of different quantities with distance.
A square-shaped coil of side 10 cm, having 100 turns is placed perpendicular to a magnetic field which is increasing at 1 T/s. The induced emf in the coil is ______.
How much charge in terms of Faraday is required for the reduction of 1 mol of Cu2+ to Cu?
