Advertisements
Advertisements
Question
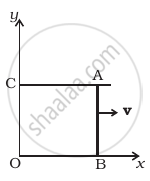
A magnetic field B = Bo sin ( ωt )`hatk` wire AB slides smoothly over two parallel conductors separated by a distance d (Figure). The wires are in the x-y plane. The wire AB (of length d) has resistance R and the parallel wires have negligible resistance. If AB is moving with velocity v, what is the current in the circuit. What is the force needed to keep the wire moving at constant velocity?
Solution
In this problem, the emf induced across AB is motional emf due to its motion, and emf induced by change in magnetic flux linked with the loop change due to a change of magnetic field.
In figure CA and OB are long parallel conducting wires, connected by d and conductor CO. The resistance of ACOB is negligible.
Let wire AB at t = 0 is at x = 0 i.e., on Y-axis.
Now AB moves with velocity `vhati`
Let at any time t, position of conductor AB is x(t) = `vhati t`
Motional e.m.f across AB
`V_(AB) = (W_(AB))/q = (D.d)/q = (qvi xx B)/q d`
`V_(AB) = vhati xx B_0 sin ωt. hatk xx d`
⇒ `e_1 = (B_0 sin ωt)vd (-hatj)`
And emf due to change in field (along OBAC)
`e_2 = (d(phi_B))/(dt)`
`phi_B = (B_0 sin ωt)(x(t)d)` ....(where, area A = xd)
`e_2 = - B_0 ω cos wtx(t)d`
Total emf in the circuit = emf due to change in field (along OBAC) + the emotional emf across AB
`e_1 + e_2 = - B_0d [ωx cos (t) + v sin (ωt)]`
The equivalent electrical diagram is shown in the diagram below.
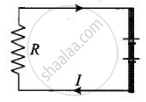
Electric current in clockwise direction is given by
= `(B_0d)/R (ωx cos ωt + v sin ωt)`
The force acting on the conductor is given by F = `ilB` sin 90° = `ilB`
Substituting the values,
`vecF_m = (B_0d)/R (ωx cos ωt + v sin ωt)(d)(B_0 sin ωt)(-hati)`
External force needed on wire is along positive x-axis to keep moving it with constant velocity is given by,
`vecF_(ext) = (B_0^2d^2)/R (ωx cos ωt + v sin ωt)sin ωt(hati)`
This is the required expression for force.
APPEARS IN
RELATED QUESTIONS
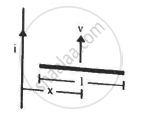
Figure shows a straight, long wire carrying a current i and a rod of length l coplanar with the wire and perpendicular to it. The rod moves with a constant velocity v in a direction parallel to the wire. The distance of the wire from the centre of the rod is x. Find the motional emf induced in the rod.
A straight conductor of length 2 m moves in a uniform magnetic field of induction 2.5 x `10^-3` T with a velocity. of 4 m/s in a direction perpendicular to its length and also perpendicular to the field. The e.m.f. induced between the ends of the conductor is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
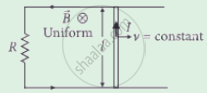
A conducting rod of length l is moving in a transverse magnetic field of strength B with velocity v. The resistance of the rod is R. The current in the rod is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
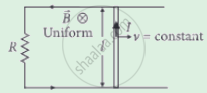
A bicycle generator creates 1.5 V at 15 km/hr. The EMF generated at 10 km/hr is ______.
Motional e.m.f is the induced e.m.f. ______
An e.m.f is produced in a coil, which is not connected to an external voltage source. This can be due to ______.
- the coil being in a time varying magnetic field.
- the coil moving in a time varying magnetic field.
- the coil moving in a constant magnetic field.
- the coil is stationary in external spatially varying magnetic field, which does not change with time.
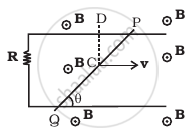
Find the current in the wire for the configuration shown in figure. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper. θ is a fixed angle made by PQ travelling smoothly over two conducting parallel wires separated by a distance d.
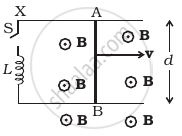
Find the current in the sliding rod AB (resistance = R) for the arrangement shown in figure. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.
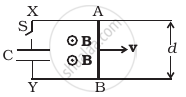
Find the current in the sliding rod AB (resistance = R) for the arrangement shown in figure. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.