Advertisements
Advertisements
Question
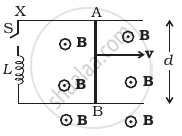
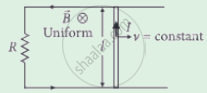
Find the current in the sliding rod AB (resistance = R) for the arrangement shown in figure. B is constant and is out of the paper. Parallel wires have no resistance. v is constant. Switch S is closed at time t = 0.
Solution
This is a similar problem as we discussed above. Here, a conductor of length d moves with speed v, perpendicular to magnetic field B as shown in figure.
Due to this, an motional emf is induced across two ends of rod (e = vBd).
Since, switch S is closed at time t = 0 current starts growing in the inductor by the potential difference due to motional emf.
By applying KVL in the given circuit, we have
`- L (dI)/(dt) + vBd = IR` or `L (dI)/(dt) + IR = vBd`
This is the linear differential equation.
On solving, we get
`I = (vBd)/R + Ae^((- Rt)/2)`
At t = 0, I = 0
⇒ `A = - (vBd)/R`
⇒ `I = (vBd)/R (1 - e^((- Rt)/L))`
This is the required expression of current.
APPEARS IN
RELATED QUESTIONS
A 20 cm long conducting rod is set into pure translation with a uniform velocity of 10 cm s−1 perpendicular to its length. A uniform magnetic field of magnitude 0.10 T exists in a direction perpendicular to the plane of motion. (a) Find the average magnetic force on the free electrons of the rod. (b) For what electric field inside the rod, the electric force on a free elctron will balance the magnetic force? How is this electric field created? (c) Find the motional emf between the ends of the rod.
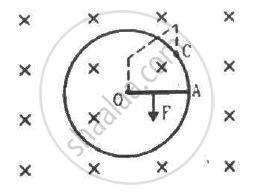
Consider the situation shown in the figure. Suppose the wire connecting O and C has zero resistance but the circular loop has a resistance Runiformly distributed along its length. The rod OA is made to rotate with a uniform angular speed ω as shown in the figure. Find the current in the rod when ∠ AOC = 90°.
A cycle wheel of radius 0.6 m is rotated with constant angular velocity of 15 rad/s in a region of magnetic field of 0.2 T which is perpendicular to the plane of the wheel. The e.m.f generated between its center and the rim is, ____________.
A conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular to one of its side. A magnetic induction B constant in time and space, pointing perpendicular and into the plane of the loop exists everywhere. The current induced in the loop is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
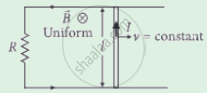
A conducting rod of length l is moving in a transverse magnetic field of strength B with velocity v. The resistance of the rod is R. The current in the rod is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
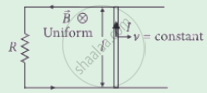
A 0.1 m long conductor carrying a current of 50 A is held perpendicular to a magnetic field of 1.25 mT. The mechanical power required to move the conductor with a speed of 1 ms-1 is ______.
The emf induced across the ends of a conductor due to its motion in a magnetic field is called motional emf. It is produced due to magnetic Lorentz force acting on the free electrons of the conductor. For a circuit shown in the figure, if a conductor of length l moves with velocity v in a magnetic field B perpendicular to both its length and the direction of the magnetic field, then all the induced parameters are possible in the circuit.
A bicycle generator creates 1.5 V at 15 km/hr. The EMF generated at 10 km/hr is ______.
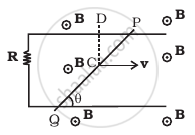
Find the current in the wire for the configuration shown in figure. Wire PQ has negligible resistance. B, the magnetic field is coming out of the paper. θ is a fixed angle made by PQ travelling smoothly over two conducting parallel wires separated by a distance d.
A rod of mass m and resistance R slides smoothly over two parallel perfectly conducting wires kept sloping at an angle θ with respect to the horizontal (Figure). The circuit is closed through a perfect conductor at the top. There is a constant magnetic field B along the vertical direction. If the rod is initially at rest, find the velocity of the rod as a function of time.

A wire 5 m long is supported horizontally at a height of 15 m along an east-west direction. When it is about to hit the ground, calculate the average e.m.f. induced in it. (g = 10 m/s2)
