Advertisements
Advertisements
Question
A metallic ring of mass m and radius `l` (ring being horizontal) is falling under gravity in a region having a magnetic field. If z is the vertical direction, the z-component of magnetic field is Bz = Bo (1 + λz). If R is the resistance of the ring and if the ring falls with a velocity v, find the energy lost in the resistance. If the ring has reached a constant velocity, use the conservation of energy to determine v in terms of m, B, λ and acceleration due to gravity g.
Solution
In this problem a relation is established between induced current, power lost and velocity acquired by freely falling ring.
The magnetic flux linked with the metallic ring of mass m and radius l ring being horizontal falling under gravity in a region having a magnetic field whose z-component of magnetic field is Bz = B0(1 + λz) is `phi = vecB_z.vecA = B_o (1 + λz).pil^2`
The angle between `vecB` and `vecA` is 0°
`ε = d/(dt) [B_o (1 + λz)]pil^2`
`IR = (B_opil^2)[0 + λ (dz)/(dt)]`
`I = (B_opiλl^2)/R (dz)/(dt) = (B_opiλl^2)/R v`
Energy lost = `I^2R = (B_o^2pi^2λ^2l^4)/R^2 v^2R`
Energy lost = `(B_o^2pi^2λ^2l^4v^2)/R`
The energy must come from decrease in P.E = `mg (dz)/(dt) = mgv`
∴ `mgv = (B_o^2pi^2λ^2v^2l^4)/R`
`v = (mgR)/(B_o^2pi^2λ^2l^4)` or `(mgR)/((pil^2λB_o)^2)`
It is the required relation.
APPEARS IN
RELATED QUESTIONS
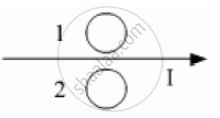
Predict the directions of induced currents in metal rings 1 and 2 lying in the same plane where current I in the wire is increasing steadily.
Predict the direction of induced current in a metal ring when the ring is moved towards a straight conductor with constant speed v. The conductor is carrying current I in the direction shown in the figure.
A pivoted aluminium bar falls much more slowly through a small region containing a magnetic field than a similar bar of an insulating material. Explain.
Two circular loops of equal radii are placed coaxially at some separation. The first is cut and a battery is inserted in between to drive a current in it. The current changes slightly because of the variation in resistance with temperature. During this period, the two loops _______________ .
Explain, with the help of a suitable example, how we can show that Lenz's law is a consequence of the principle of conservation of energy.
Consider a metal ring kept (supported by a cardboard) on top of a fixed solenoid carrying a current I (Figure). The centre of the ring coincides with the axis of the solenoid. If the current in the solenoid is switched off, what will happen to the ring?

A conducting wire XY of mass m and neglibile resistance slides smoothly on two parallel conducting wires as shown in figure. The closed circuit has a resistance R due to AC. AB and CD are perfect conductors. There is a ˆ. magnetic field `B = B(t)hatk`.
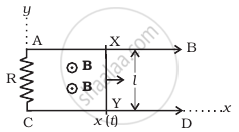
- Write down equation for the acceleration of the wire XY.
- If B is independent of time, obtain v(t) , assuming v(0) = u0.
- For (b), show that the decrease in kinetic energy of XY equals the heat lost in R.
A long solenoid ‘S’ has ‘n’ turns per meter, with diameter ‘a’. At the centre of this coil we place a smaller coil of ‘N’ turns and diameter ‘b’ (where b < a). If the current in the solenoid increases linearly, with time, what is the induced emf appearing in the smaller coil. Plot graph showing nature of variation in emf, if current varies as a function of mt2 + C.
Predict the direction of induced current in the situation described by the following figure.