Advertisements
Advertisements
Question
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant k1 and the other has thickness d2 and dielectric constant k2 as shown in figure. This arrangement can be thought as a dielectric slab of thickness d (= d1 + d2) and effective dielectric constant k. The k is ______.
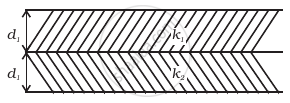
Options
`(k_1d_1 + k_2d_2)/(d_1 + d_2)`
`(k_1d_1 + k_2d_2)/(k_1 + k_2)`
`(k_1k_2 (d_1 + d_2))/((k_1d_1 + k_2d_2))`
`(2k_1k_2)/(k_1 + k_2)`
Solution
A parallel plate capacitor is made of two dielectric blocks in series. One of the blocks has thickness d1 and dielectric constant k1 and the other has thickness d2 and dielectric constant k2 as shown in figure. This arrangement can be thought as a dielectric slab of thickness d (= d1 + d2) and effective dielectric constant k. The k is `underline((k_1k_2 (d_1 + d_2))/((k_1d_1 + k_2d_2)))`.
Explanation:
Here the system can be considered as two capacitors C1 and C2 connected in series as shown in figure.
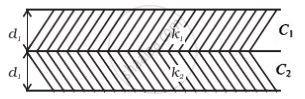
The capacitance of parallel plate capacitor filled with dielectric block has thickness d1 and dielectric constant K2 is given by
`1/C_(eq) = 1/C_1 + 1/C_2` ⇒ `C_(eq) = (C_1C_2)/(C_1 + C_2)`
`C_(eq) = ((k_1ε_0A)/(d_1))/((k_1ε_0A)/(d_1)) ((k_2ε_0A)/(d_2))/((k_2ε_0A)/(d_2)) = (k_1k_2ε_0A)/(k_1d_2 + k_2d_1)` ......(i)
We can write the equivalent capacitance as `C = (kε_0A)/(d_1 + d_2)` ......(ii)
On comparing (i) and (ii) we have
`k = (k_1k_2(d_1 + d_2))/(k_1d_2 + k_2d_1)`
APPEARS IN
RELATED QUESTIONS
Obtain an expression for electric field intensity at a point outside uniformly charged thin plane sheet.
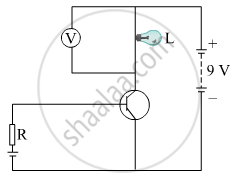
In the given circuit diagram a voltmeter ‘V’ is connected across a lamp ‘L’. Ho would (i) the brightness of the lamp and (ii) voltmeter reading ‘V’ be affected, if the value of resistance ‘R’ is decreased? Justify your answer.
A 10 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 38Ω as shown in the figure. Find the value of the current in circuit.

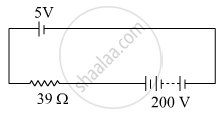
A 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current in circuit.
If the above capacitor is connected across a 6⋅0 V battery, find (a) the charge supplied by the battery, (b) the induced charge on the dielectric and (c) the net charge appearing on one of the coated surfaces.
A capacitor has some dielectric between its plates, and the capacitor is connected to a dc source. The battery is now disconnected and then the dielectric is removed, then ______.
A capacitor is made of two circular plates of radius R each, separated by a distance d << R. The capacitor is connected to a constant voltage. A thin conducting disc of radius r<<R and thickness t << r is placed at a centre of the bottom plate. Find the minimum voltage required to lift the disc if the mass of the disc is m.
