Advertisements
Advertisements
Question
A ray of light, incident on an equilateral prism `(μ_g = sqrt3)`moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
Solution
It is given that the prism is equilateral in shape. So, all the angles are equal to 60°.
Thus, the angle of prism, A = 60°
The angle of refraction in case of a prism, `r =A/2 = 30°`
We can now apply Snell’s law
So,
μa sin i = μg sin r
Here, μa → refractive index of air, n1 = 1
μg → refractive index of glass,`n_2 =sqrt3`
i → angle of incidence
Thus,
`sin i = ((mug)/mu_a) sin r ((mug)/mu_a) sin 30° `
`sin i = sqrt3/2`
So, the angle of incidence is
i =60°
APPEARS IN
RELATED QUESTIONS
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light? Give reason.
Three rays (1, 2, 3) of different colours fall normally on one of the sides of an isosceles right angled prism as shown. The refractive index of prism for these rays is 1.39, 1.47 and 1.52 respectively. Find which of these rays get internally reflected and which get only refracted from AC. Trace the paths of rays. Justify your answer with the help of necessary calculations.
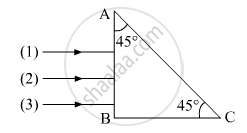
Three light rays red (R), green (G) and blue (B) are incident on a right angled prism ‘abc’ at face ‘ab’. The refractive indices of the material of the prism for red, green and blue wavelengths are 1.39, 1.44 and 1.47 respectively. Out of the three which colour ray will emerge out of face ‘ac’? Justify your answer. Trace the path of these rays after passing through face ‘ab’.
Can you ever have a situation in which a light ray goes undeviated through a prism?
A flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0°, what would be the refracting angle of the crown prism?
A small object is embedded in a glass sphere (μ = 1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
Answer the following question.
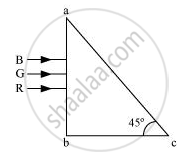
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index `sqrt(3)`. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air?
The refractive index of a prism whose angle A = 60° is `sqrt2`. Then the angle of minimum deviation δm will be ______.
Two concave refracting surfaces of equal radii of curvature face each other in the air as shown in the figure. The point object O is placed midway between the centre and one of the poles. Then the separation between the images of O formed by each refracting surface is ______.
A ray of monochromatic light passes through an equilateral glass prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 3/4 times the angle of the prism. Determine the angle of deviation and the refractive index of the glass prism.
