Advertisements
Advertisements
Question
A ray of monochromatic light passes through an equilateral glass prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 3/4 times the angle of the prism. Determine the angle of deviation and the refractive index of the glass prism.
Solution
Here the angle of prism A = 60°, the angle of incidence i = angle of emergence e and under this condition angle of deviation is minimum.
∴ i = e = `3/4` A = `3/4 xx 60^circ = 45^circ` and i + e = A + D,
hence Dm = 2i - A = 2 × 45° - 60° = 30°
The refractive index of the glass prism,
n = `sin((A + D_m)/2)/(sin(A/2)) = (sin((60^circ + 30^circ)/2))/(sin(60^circ/2))`
= `(sin45^circ)/(sin30^circ) = (1/sqrt2)/(1/2) = sqrt2`
APPEARS IN
RELATED QUESTIONS
Find the angle of incidence at face AB so that the emergent ray grazes along the face AC.
Write the relationship between angle of incidence ‘i’, angle of prism ‘A’ and angle of minimum deviations for a triangular prism.
Can you ever have a situation in which a light ray goes undeviated through a prism?
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
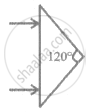
An isosceles prism of angle 120° has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite faces:
For a glass prism `(µ = sqrt(3))` the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
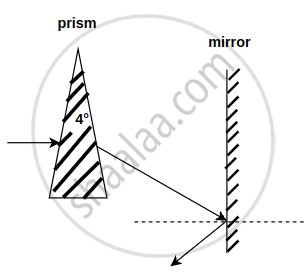
A horizontal ray of light passes through a prism of index 1.50 and apex angle 4° and then strikes a vertical mirror, as shown in the figure (a). Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is ______.
A ray of light when incident upon a thin prism suffers a minimum deviation of 39°. If the shaded half portion of the prism is removed, then the same ray will ______.
Two concave refracting surfaces of equal radii of curvature face each other in the air as shown in the figure. The point object O is placed midway between the centre and one of the poles. Then the separation between the images of O formed by each refracting surface is ______.