Advertisements
Advertisements
Question
A prism is made of glass of unknown refractive index. A parallel beam of light is incident on the face of the prism. The angle of minimum deviation is measured to be 40°. What is the refractive index of the material of the prism? The refracting angle of the prism is 60°. If the prism is placed in water (refractive index 1.33), predict the new angle of minimum deviation of a parallel beam of light.
Solution
Angle of minimum deviation, δm = 40°
Angle of the prism, A = 60°
Refractive index of water, µ = 1.33
Refractive index of the material of the prism = µ'
The angle of deviation is related to refractive index (µ') as:
µ' = `(sin (("A" + δ_"m"))/2)/(sin "A"/2)`
= `(sin ((60° + 40°))/2)/(sin (60°)/2)`
= `(sin 50°)/(sin 30°)`
= 1.532
Hence, the refractive index of the material of the prism is 1.532.
Since the prism is placed in water, let `δ_"m"^"'"` be the new angle of minimum deviation for the same prism.
The refractive index of glass with respect to water is given by the relation:
`μ_"g"^"w" = (μ"'")/μ = (sin (("A" + δ_"m"^"'"))/2)/(sin "A"/2)`
`sin (("A" + δ_"m"^"'"))/2 = (μ"'")/μ sin "A"/2`
`sin (("A" + δ_"m"^"'"))/2 = 1.532/1.33 xx sin (60°)/2 = 0.5759`
` (("A" + δ_"m"^"'"))/2 = sin^-1 0.5759` = 35.16°
60° + `δ_"m"^"'"` = 70.32°
∴ `δ_"m"^"'"` = 70.32° − 60° = 10.32°
Hence, the new minimum angle of deviation is 10.32°.
APPEARS IN
RELATED QUESTIONS
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced by red light? Give reason.
Three rays (1, 2, 3) of different colours fall normally on one of the sides of an isosceles right angled prism as shown. The refractive index of prism for these rays is 1.39, 1.47 and 1.52 respectively. Find which of these rays get internally reflected and which get only refracted from AC. Trace the paths of rays. Justify your answer with the help of necessary calculations.
Find the angle of minimum deviation for an equilateral prism made of a material of refractive index 1.732. What is the angle of incidence for this deviation?
A small object is embedded in a glass sphere (μ = 1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
The refractive index of a prism whose angle A = 60° is `sqrt2`. Then the angle of minimum deviation δm will be ______.
For a glass prism `(µ = sqrt(3))` the angle of minimum deviation is equal to the angle of the prism. Find the angle of the prism.
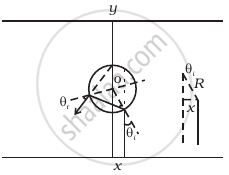
An infinitely long cylinder of radius R is made of an unusual exotic material with refractive index –1 (Figure). The cylinder is placed between two planes whose normals are along the y direction. The center of the cylinder O lies along the y-axis. A narrow laser beam is directed along the y direction from the lower plate. The laser source is at a horizontal distance x from the diameter in the y direction. Find the range of x such that light emitted from the lower plane does not reach the upper plane.
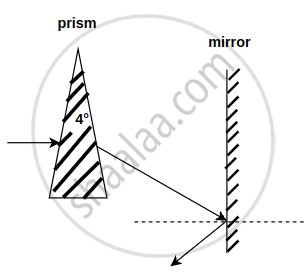
A horizontal ray of light passes through a prism of index 1.50 and apex angle 4° and then strikes a vertical mirror, as shown in the figure (a). Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
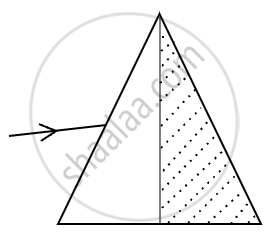
A ray of light when incident upon a thin prism suffers a minimum deviation of 39°. If the shaded half portion of the prism is removed, then the same ray will ______.
A ray of light is refracted by a glass prism. Obtain an expression for the refractive index of the glass in terms of the angle of prism A and the angle of minimum deviation δm.
