Advertisements
Advertisements
Question
A ray of light is refracted by a glass prism. Obtain an expression for the refractive index of the glass in terms of the angle of prism A and the angle of minimum deviation δm.
Solution
In the given diagram,
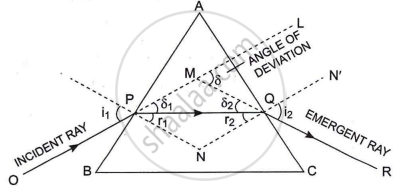
OP is the incident ray, which makes the angle i1 normal, and ∠N'QR is the angle of emergence, which is represented by i2. A is the prism angle, and µ is the refractive index of the prism.
A = Prism angle, δ = Angle of deviation, i1 = Angle of incidence, i2 = Angle of emergence.
In the case of minimum deviation,
`∠r_1 = ∠r_2 = ∠r`
A = `∠r_1 + ∠r_2`
So, A = ∠r + ∠r = ∠2r
∠r = `A/2`
Now, again
A + δ = i1 + i2 ....(∵ In the case of minimum deviation i1 = i2 = i and δ = δm)
So, A + δm = i + i = 2i
Now, `i = ((A + δ_m))/2`
Now, from Snell's rule,
`mu = (sini)/(sinr)`
`mu = (sin((A + delta_m)/2))/(sin A/2)`
APPEARS IN
RELATED QUESTIONS
At what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524.
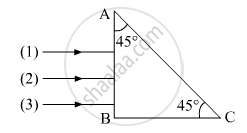
Three rays (1, 2, 3) of different colours fall normally on one of the sides of an isosceles right angled prism as shown. The refractive index of prism for these rays is 1.39, 1.47 and 1.52 respectively. Find which of these rays get internally reflected and which get only refracted from AC. Trace the paths of rays. Justify your answer with the help of necessary calculations.
A ray of light, incident on an equilateral prism `(μ_g = sqrt3)`moves parallel to the base line of the prism inside it. Find the angle of incidence for this ray.
If a piece of paper is placed at the position of a virtual image of a strong light source, will the paper burn after sufficient time? What happens if the image is real? What happens if the image is real but the source is virtual?
Suggest a method to produce a rainbow in your house.
Answer the following question.
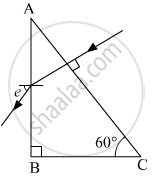
Calculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index `sqrt(3)`. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air?
Two prisms ABC and DBC are arranged as shown in the figure.

The critical angles for the two prisms with respect to air are 41.1° and 45° respectively. Trace the path of the ray through the combination.
The maximum value of the index of refraction of a material of a prism which allows the passage of light through it when the refracting angle of the prism is A is ______.
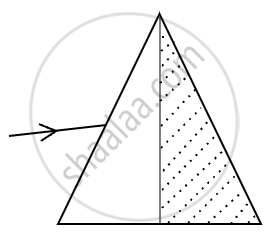
A ray of light when incident upon a thin prism suffers a minimum deviation of 39°. If the shaded half portion of the prism is removed, then the same ray will ______.
A ray of monochromatic light passes through an equilateral glass prism in such a way that the angle of incidence is equal to the angle of emergence and each of these angles is 3/4 times the angle of the prism. Determine the angle of deviation and the refractive index of the glass prism.
