Advertisements
Advertisements
Question
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
Solution
Actual depth of the bulb in water, d1 = 80 cm = 0.8 m
Refractive index of water, μ = 1.33
The given situation is shown in the following figure:
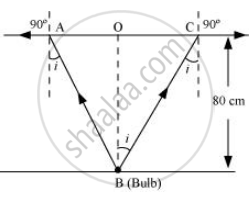
Where,
i = Angle of incidence
r = Angle of refraction = 90°
Since the bulb is a point source, the emergent light can be considered as a circle of radius, R = `"AC"/2` = AO = OB
Using Snell’ law, we can write the relation for the refractive index of water as:
μ = `(sin "r")/(sin "i")`
1.33 = `(sin 90°)/(sin "i")`
∴ i = `sin^-1 (1/1.33)` = 48.75°
Using the given figure, we have the relation:
tan i = `"OC"/"OB" = "R"/"d"_1`
∴ R = tan 48.75° × 0.8 = 0.91 m
∴ Area of the surface of water = πR2 = π (0.91)2 = 2.61 m2
Hence, the area of the surface of water through which the light from the bulb can emerge is approximately 2.61 m2.
APPEARS IN
RELATED QUESTIONS
Derive Snell’s law on the basis of Huygen’s wave theory when the light is travelling from a denser to a rarer medium.
Calculate the speed of light in a medium whose critical angle is 45°. Does critical angle for a given pair of media depend on the wavelength of incident light ? Give reason.
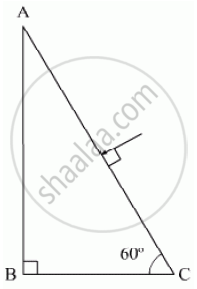
Trace the path of a ray of light passing through a glass prism (ABC) as shown in the figure. If the refractive index of glass is `sqrt3`, find out the value of the angle of emergence from the prism.
Find a critical angle for glass and water pair, given the refractive index of glass, is 1 ·62 and that of water is 1 ·33.
Define the term, “refractive index” of a medium. Verify Snell’s law of refraction when a plane wavefront is propagating from a denser to a rarer medium. Solution
According to Snell’s law, ______.
For small angles Snell’s law becomes ______.
Draw the shape of refracted wavefront when the plane incident wave undergoes refraction from optically denser medium to rarer medium. Hence prove Snell’s law of refraction.
The mixture a pure liquid and a solution in a long vertical column (i.e, horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d << h, the height of the column.
If light passes near a massive object, the gravitational interaction causes a bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by n(r) = 1 + 2 GM/rc2 where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
