Advertisements
Advertisements
Question
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
Advertisements
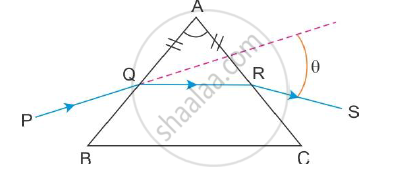
Solution
The angle of the prism is A = 60°. It is also given that AQ = AR. Therefore, the angles opposite to these two sides are also equal.
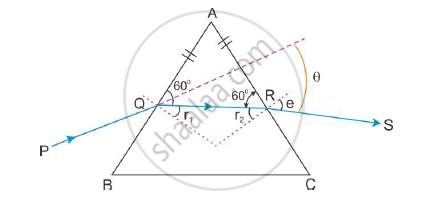
∠AQR = ∠ARQ
Now, for a triangle
∠A + ∠AQR + ∠ARQ = 180°
∴ ∠AQR = ∠ARQ = 60°
∴ r1=r2 = 30° (∠AQO = ∠ARO = 90°)
∴ r1 + r2 = 60°
When r1 and r2 are equal, we have i = e. Now, according to Snell’s law,
`mu=sini/sinr_1`
`:.sini=musinr_1=sqrt3 sin30 =sqrt3/2`
∴ i = 60°
Now, the angle of deviation θ is
θ = i + e - A
∴ θ = 60 + 60 -60
∴ θ = 60°
APPEARS IN
RELATED QUESTIONS
A ray of light passes through an equilateral glass prism such that the angle of incidence is equal to the angle of emergence and each of these angles is equal to 3/4 of angle of prism. Find the angle of deviation.
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays '1' and '2' are respectively 1.38 and 1.52. Trace the path of these rays after entering through the prism.
What is the cause of dispersion of light
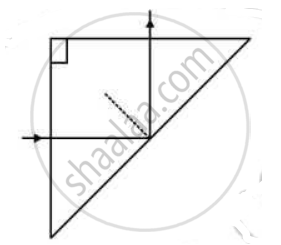
A ray of light incident normally on one face of a right isosceles prism is totally reflected, as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.
If three identical prisms are combined, is it possible to pass a beam that emerges undeviated? Undispersed?
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
The minimum deviations suffered by, yellow and violet beams passing through an equilateral transparent prism are 38.4°, 38.7° and 39.2° respectively. Calculate the dispersive power of the medium.
The deviation produced for violet, yellow and red lights for crown glass are 3.75°, 3.25° and 2.86° respectively. Calculate the dispersive power of the crown glass.
In a regular prism, what is the relation between angle of incidence and angle of emergence when it is in the minimum deviation position?
Prove that in case of a prism, i + e = A + δ, where the symbols have their usual meanings.
