Advertisements
Advertisements
Question
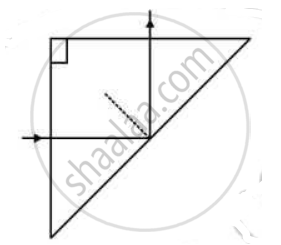
A ray of light incident normally on one face of a right isosceles prism is totally reflected, as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.
Solution

We know that light incident normally on one face of a right isosceles prism is totally reflected.
`mu=1/sin C " "("Total internal reflection")`
C is the critical angle, which is 45º
`mu=1/sin 45`
`mu=sqrt2=1.41`
Thus, the minimum value of the refractive index of the glass is 1.41.
RELATED QUESTIONS
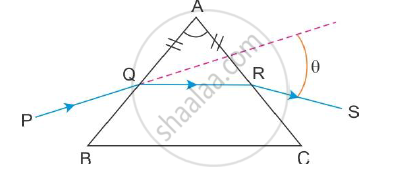
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
What is a dispersion of light
What is the cause of dispersion of light
Draw the ray diagram showing refraction of light through a glass prism and hence obtain the relation between the refractive index μ of the prism, angle of prism and angle of minimum deviation.
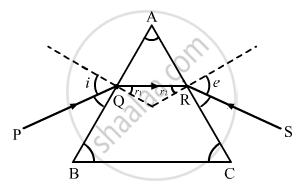
Figure shows a ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, show that (i) r1 = r2 = A/2 and (ii) angle of minimum deviation, Dm = 2i − A.
The equation \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] was derived for a prism having small refracting angle. Is it also valid for a prism of large refracting angle? Is it also valid for a glass slab or a glass sphere?
Can the dispersive power \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] be negative? What is the sign of ω if a hollow prism is immersed into water?
A certain material has refractive indices 1.56, 1.60 and 1.68 rfor red, yellow and violet lightespectively. (a) Calculate the dispersive power. (b) Find the angular dispersion produced by a thin prism of angle 6° made of this material.
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
How does the angle of minimum deviation of a glass prism vary if the incident violet light is replaced by red light?
