Advertisements
Advertisements
Question
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
Solution
Expression for Fringe Width in Young’s Double-Slit Experiment
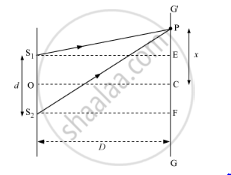
Let S1 and S2 be two slits separated by a distance d. `GG'` is the screen at a distance D from the slits S1and S2. Point C is equidistant from both the slits. The intensity of light will be maximum at this point because the path difference of the waves reaching this point will be zero.
At point P, the path difference between the rays coming from the slits is given by
S1= S2P − S1P
Now, S1 S2 = d, EF = d, and S2F = D
In ΔS2PF,
`S_2P=[S_2F^2+PF^2]^(1/2)`
`S_2P=[D2+(x+d/2)^2]^(1/2)`
`=D[1+(x+d/2)^2/D^2]^(1/2)`
Similarly, in ΔS1PE
`S_1P=D[1+(x-d/2)^2/D^2]^(1/2)`
`:.S_2P-S_1P=D[1+1/2(x+d/2)^2/D^2)]-D[1+1/2(x-d/2)^2/D^2]`
On expanding it binomially, we get
`S_2P-S_1P=1/(2D)[4xd/2]=(xd)/D`
For constructive interference, the path difference is an integral multiple of wavelengths, that is, path difference is nλ.
`:.nlambda=(xd)/D`
`x=(nlambdaD)/d`
where n = 0, 1, 2, 3, 4, …
Similarly, for destructive interference,
`x_n=(2n-1)lambda/2D/d`
Graph of Intensity Distribution in Young’s Double-Slit Experiment
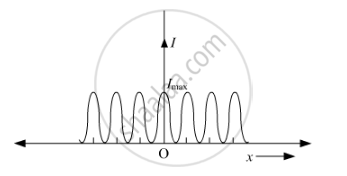
(ii) On comparing the interference pattern observed in Young's double slit experiment (interference) with single-slit diffraction pattern (diffraction), we can have three distinguishing features:
In the interference pattern, all the bright fringes have the same intensity. In a diffraction pattern, all the bright fringes are not of the same intensity
In the interference pattern, the dark fringe has zero or very small intensity so that the bright and dark fringes can easily be distinguished. In diffraction pattern, all the dark fringes are not of zero intensity
In the interference pattern, the widths of all the fringes are almost the same, whereas in diffraction pattern, the fringes are of different widths
RELATED QUESTIONS
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
What is the effect on the interference fringes to a Young’s double slit experiment when
(i) the separation between the two slits is decreased?
(ii) the width of a source slit is increased?
(iii) the monochromatic source is replaced by a source of white light?
Justify your answer in each case.
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
A Young's double slit experiment is performed with white light.
(a) The central fringe will be white.
(b) There will not be a completely dark fringe.
(c) The fringe next to the central will be red.
(d) The fringe next to the central will be violet.
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
