Advertisements
Advertisements
प्रश्न
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
Advertisements
उत्तर
Expression for Fringe Width in Young’s Double-Slit Experiment
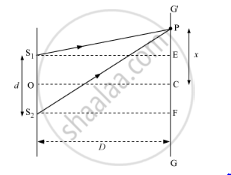
Let S1 and S2 be two slits separated by a distance d. `GG'` is the screen at a distance D from the slits S1and S2. Point C is equidistant from both the slits. The intensity of light will be maximum at this point because the path difference of the waves reaching this point will be zero.
At point P, the path difference between the rays coming from the slits is given by
S1= S2P − S1P
Now, S1 S2 = d, EF = d, and S2F = D
In ΔS2PF,
`S_2P=[S_2F^2+PF^2]^(1/2)`
`S_2P=[D2+(x+d/2)^2]^(1/2)`
`=D[1+(x+d/2)^2/D^2]^(1/2)`
Similarly, in ΔS1PE
`S_1P=D[1+(x-d/2)^2/D^2]^(1/2)`
`:.S_2P-S_1P=D[1+1/2(x+d/2)^2/D^2)]-D[1+1/2(x-d/2)^2/D^2]`
On expanding it binomially, we get
`S_2P-S_1P=1/(2D)[4xd/2]=(xd)/D`
For constructive interference, the path difference is an integral multiple of wavelengths, that is, path difference is nλ.
`:.nlambda=(xd)/D`
`x=(nlambdaD)/d`
where n = 0, 1, 2, 3, 4, …
Similarly, for destructive interference,
`x_n=(2n-1)lambda/2D/d`
Graph of Intensity Distribution in Young’s Double-Slit Experiment
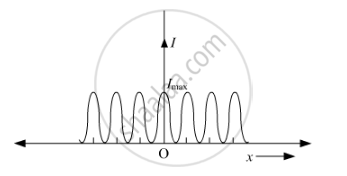
(ii) On comparing the interference pattern observed in Young's double slit experiment (interference) with single-slit diffraction pattern (diffraction), we can have three distinguishing features:
In the interference pattern, all the bright fringes have the same intensity. In a diffraction pattern, all the bright fringes are not of the same intensity
In the interference pattern, the dark fringe has zero or very small intensity so that the bright and dark fringes can easily be distinguished. In diffraction pattern, all the dark fringes are not of zero intensity
In the interference pattern, the widths of all the fringes are almost the same, whereas in diffraction pattern, the fringes are of different widths
संबंधित प्रश्न
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
What is the interference pattern observed on the screen in Young's double-slit experiment?
What is the angular fringe width \(\alpha\)?
