Advertisements
Advertisements
प्रश्न
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
उत्तर
Given:-
Refractive index of the mica sheet,μ = 1.6
Thickness of the plate,
\[t = 1 . 964 \text{ micron }= 1 . 964 \times {10}^{- 6} m\]
Let the wavelength of the light used = λ.
Number of fringes shifted is given by
\[n = \frac{\left( \mu - 1 \right)t}{\lambda}\]
So, the corresponding shift in the fringe width equals the number of fringes multiplied by the width of one fringe.
\[\text{Shift} = n \times \beta\]
\[ = \frac{\left( \mu - 1 \right)t}{\lambda} \times \frac{\lambda D}{d}\]
\[ = \frac{\left( \mu - 1 \right)t \times D}{d}..........(1)\]
As per the question, when the distance between the screen and the slits is doubled,
i.e. \[D' = 2D\]
fringe width,
\[\beta = \frac{\lambda D'}{d} = \frac{\lambda 2D}{d}\]
According to the question, fringe shift in first case = fringe width in second case.
\[\text{So, }\frac{\left( \mu - 1 \right)t \times D}{d} = \frac{\lambda2D}{d}\]
\[ \Rightarrow \lambda = \frac{\left( \mu - 1 \right) t}{2}\]
\[ = \frac{\left( 1 . 6 - 1 \right) \times \left( 1 . 964 \right) \times {10}^{- 6}}{2}\]
\[ = 589 . 2 \times {10}^{- 9} = 589 . 2\text{ nm}\]
Hence, the required wavelength of the monochromatic light is 589.2 nm.
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
The intensity at the central maxima in Young’s double slit experimental set-up is I0. Show that the intensity at a point where the path difference is λ/3 is I0/4.
White light is used in a Young's double slit experiment. Find the minimum order of the violet fringe \[\left( \lambda = 400\text{ nm} \right)\] which overlaps with a red fringe \[\left( \lambda = 700\text{ nm} \right).\]
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
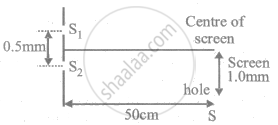
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
Two slits, 4mm apart, are illuminated by light of wavelength 6000 A° what will be the fringe width on a screen placed 2 m from the slits?
Why is the diffraction of sound waves more evident in daily experience than that of light wave?
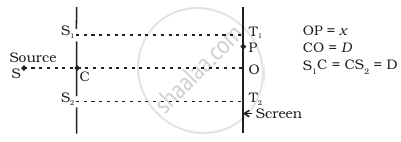
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
