Advertisements
Advertisements
प्रश्न
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
उत्तर
Given:-
Separation between the two slits,
\[d = 1 mm = {10}^{- 3} m\]
Wavelength of the light,
\[\lambda = 500 nm = 5 \times {10}^{- 7} m\]
Distance of the screen,
\[D = 1 m\]
Let Imax be the maximum intensity and I be the intensity at the required point at a distance y from the central point.
So, \[I = a^2 + a^2 + 2 a^2 \cos\phi\]
Here, \[\phi\] is the phase difference in the waves coming from the two slits.
So, \[I = 4 a^2 \cos^2 \left( \frac{\phi}{2} \right)\]
\[\Rightarrow \frac{I}{I_\max} = \frac{1}{2}\]
\[ \Rightarrow \frac{4 a^2 \cos^2 \left( \frac{\phi}{2} \right)}{4 a^2} = \frac{1}{2}\]
\[ \Rightarrow \cos^2 \left( \frac{\phi}{2} \right) = \frac{1}{2}\]
\[ \Rightarrow \cos\left( \frac{\phi}{2} \right) = \frac{1}{\sqrt{2}}\]
\[ \Rightarrow \frac{\phi}{2} = \frac{\pi}{4}\]
\[ \Rightarrow \phi = \frac{\pi}{2}\]
Corrosponding path difference, \[∆ x = \frac{1}{4}\]
\[ \Rightarrow y = \frac{∆ xD}{d} = \frac{\lambda D}{4d}\]
\[\Rightarrow y = \frac{5 \times {10}^{- 7} \times 1}{4 \times {10}^{- 3}}\]
\[ = 1 . 25 \times {10}^{- 4} m\]
∴ The required minimum distance from the central maximum is \[1 . 25 \times {10}^{- 4} m.\]
APPEARS IN
संबंधित प्रश्न
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
A source emitting light of wavelengths 480 nm and 600 nm is used in a double-slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
White coherent light (400 nm-700 nm) is sent through the slits of a Young's double slit experiment (see the following figure). The separation between the slits is 0⋅5 mm and the screen is 50 cm away from the slits. There is a hole in the screen at a point 1⋅0 mm away (along the width of the fringes) from the central line. (a) Which wavelength(s) will be absent in the light coming from the hole? (b) Which wavelength(s) will have a strong intensity?
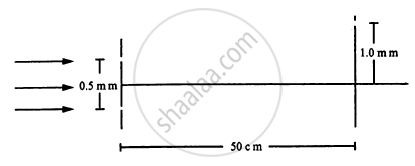
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
Two slits in Young's interference experiment have width in the ratio 1 : 2. The ratio of intensity at the maxima and minima in their interference is ______.
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
