Advertisements
Advertisements
प्रश्न
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
उत्तर
Given:-
The thickness of the strips = \[t_1 = t_2 = t = 0 . 5 mm = 0 . 5 \times {10}^{- 3} m\]
Separation between the two slits,
\[d = 0 . 12 cm = 12 \times {10}^{- 4} m\]
The refractive index of mica, μm = 1.58 and of polystyrene, μp = 1.58
Wavelength of the light,
\[\lambda = 590 nm = 590 \times {10}^{- 9} m,\]
Distance between screen and slit, D = 1 m
(a)
We know that fringe width is given by
\[\beta = \frac{\lambda D}{d}\]
\[\Rightarrow \beta = \frac{590 \times {10}^{- 9} \times 1}{12 \times {10}^{- 4}}\]
\[= 4 . 9 \times {10}^{- 4} m\]
(b) When both the mica and polystyrene strips are fitted before the slits, the optical path changes by
\[∆ x = \left( \mu_m - 1 \right) t - \left( \mu_p - 1 \right) t\]
\[= \left( \mu_m - \mu_p \right) t\]
\[ = \left( 1 . 58 - 1 . 55 \right) \times \left( 0 . 5 \right) \left( {10}^{- 3} \right)\]
\[ = \left( 0 . 015 \right) \times {10}^{- 3} m\]
∴ Number of fringes shifted, n = \[\frac{∆ x}{\lambda}\]
\[\Rightarrow n = \frac{0 . 015 \times {10}^{- 3}}{590 \times {10}^{- 9}} = 25 . 43\]
∴ 25 fringes and 0.43th of a fringe.
⇒ In which 13 bright fringes and 12 dark fringes and 0.43th of a dark fringe.
So, position of first maximum on both sides is given by
On one side,
\[x = \left( 0 . 43 \right) \times 4 . 91 \times {10}^{- 4}...........\left( \because \beta = 4 . 91 \times {10}^{- 4} m \right)\]
\[= 0 . 021 cm\]
On the other side,
\[x' = \left( 1 - 0 . 43 \right) \times 4 . 91 \times {10}^{- 4} \]
\[ = 0 . 028 cm\]
APPEARS IN
संबंधित प्रश्न
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
Two coherent sources of light having intensity ratio 81 : 1 produce interference fringes. Calculate the ratio of intensities at the maxima and minima in the interference pattern.
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
In Young’s double slit experiment, what is the effect on fringe pattern if the slits are brought closer to each other?
In Young's double slit experiment the slits are 0.589 mm apart and the interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 7.5 mm from the dark fringe which is second from the center of the fringe pattern. Find the wavelength of the light used.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
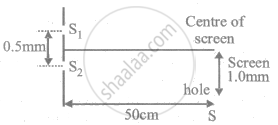
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
A slit of width 0.6 mm is illuminated by a beam of light consisting of two wavelengths 600 nm and 480 nm. The diffraction pattern is observed on a screen 1.0 m from the slit. Find:
- The distance of the second bright fringe from the central maximum pertaining to the light of 600 nm.
- The least distance from the central maximum at which bright fringes due to both wavelengths coincide.
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of the fourth bright fringe after a glass plate of refractive index 1.5 is introduced in the path of one of the beams. The thickness of the glass plate would be ______.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
