Advertisements
Advertisements
प्रश्न
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
उत्तर
For any other incoherent source of light a steady interference pattern can never be obtained, even if the sources emit waves of equal wavelengths and equal amplitudes. This is because the waves emitted by a source undergo rapid and irregular changes of phase, so that the intensity at any point is never constant. Naturally the phase difference between the waves emitted by the two sources cannot remain constant.
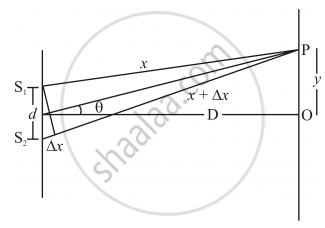
The two waves interfering at P have different distances S1P = x and S2P = x + Δx.
So, for the two sources S1 and S2we can respectively write,
`I_1 = I_(01) sin (kx -wt)`
`I_1 = I_(02) sin (k(x +Deltax)-wt) =I_(02)sin(kx -wt +delta)`
`delta = kDeltax =((2pi)/lambda) xx Delta x`
The resultant can be written as,
`I =I_0sin(kx -wt +epsi)
Where` I_0^2 =I_(01)^2 + I_(02)^2 +2I_(01) I_(02) cos delta`
And tan`epsi = I_(02) sin delta /(I_(01) +I_(02)cos delta)`
The condition for constructive (bright fringe) and destructive (dark fringe) interference are as follows;
δ = 2nπ for bright fringes
δ = (2n + 1) π for dark fringes
Where n is an integer.
Now to find the fringe width,
The path difference is `Deltax =S_2P-S_1P` nearly equal to d `sintheta =d tantheta =(dy)/D`
Hence we can write, `y=(nlambdaD)/d ,n` is an integer.
APPEARS IN
संबंधित प्रश्न
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
A source emitting light of wavelengths 480 nm and 600 nm is used in a double-slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
In Young's double-slit experiment, the screen is moved away from the plane of the slits. What will be its effect on the following?
- The angular separation of the fringes.
- Fringe-width.
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
