Advertisements
Advertisements
प्रश्न
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
उत्तर
Given:-
Fours slits S1, S2, S3 and S4.
The separation between slits S3 and S4 can be changed.
Point P is the common perpendicular bisector of S1S2 and S3S4.
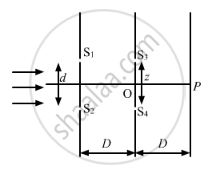
(a) For \[z = \frac{\lambda D}{d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{\lambda D}{2d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]
Similarly at S4, path difference, \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]
i.e. dark fringes are formed at S3 and S4.
So, the intensity of light at S3 and S4 is zero. Hence, the intensity at P is also zero.
(b) For \[z = \frac{3\lambda D}{2d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{3\lambda D}{4d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]
Similarly at S4, path difference,
\[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]
Hence, the intensity at P is I.
(c) For \[z = \frac{2\lambda D}{d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{2\lambda D}{2d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]
Similarly at S4, path difference, \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]
Hence, the intensity at P is 2I.
APPEARS IN
संबंधित प्रश्न
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
How does an unpolarized light incident on a polaroid get polarized? Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
If Young's double slit experiment is performed in water, _________________ .
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
A parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Slow that if the incident beam makes an angle \[\theta = \sin^{- 1} \left( \frac{\lambda}{2d} \right)\] with the normal to the plane of the slits, there will be a dark fringe at the centre P0 of the pattern.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
Two slits in Young's interference experiment have width in the ratio 1 : 2. The ratio of intensity at the maxima and minima in their interference is ______.
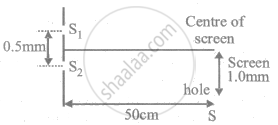
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
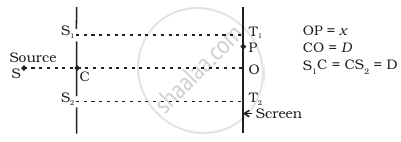
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
