Advertisements
Advertisements
प्रश्न
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to
(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
Advertisements
उत्तर
Given:-
Fours slits S1, S2, S3 and S4.
The separation between slits S3 and S4 can be changed.
Point P is the common perpendicular bisector of S1S2 and S3S4.
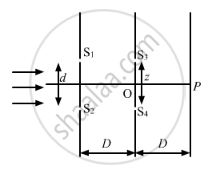
(a) For \[z = \frac{\lambda D}{d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{\lambda D}{2d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]
Similarly at S4, path difference, \[∆ x = \frac{yd}{D} = \frac{\lambda D}{2d} \times \frac{d}{D} = \frac{\lambda}{2}\]
i.e. dark fringes are formed at S3 and S4.
So, the intensity of light at S3 and S4 is zero. Hence, the intensity at P is also zero.
(b) For \[z = \frac{3\lambda D}{2d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{3\lambda D}{4d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]
Similarly at S4, path difference,
\[∆ x = \frac{yd}{D} = \frac{3\lambda D}{4d} \times \frac{d}{D} = \frac{3\lambda}{4}\]
Hence, the intensity at P is I.
(c) For \[z = \frac{2\lambda D}{d}\]
The position of the slits from the central point of the first screen is given by \[y = {OS}_3 = {OS}_4 = \frac{z}{2} = \frac{2\lambda D}{2d}\]
The corresponding path difference in wave fronts reaching S3 is given by \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]
Similarly at S4, path difference, \[∆ x = \frac{yd}{D} = \frac{2\lambda D}{2d} \times \frac{d}{D} = \lambda\]
Hence, the intensity at P is 2I.
APPEARS IN
संबंधित प्रश्न
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
Find the intensity at a point on a screen in Young's double slit experiment where the interfering waves have a path difference of (i) λ/6, and (ii) λ/2.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
How does an unpolarized light incident on a polaroid get polarized? Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
Wavefront is ______.
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
