Advertisements
Advertisements
प्रश्न
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
उत्तर
Given:-
Refractive index of the two slabs are µ1 and µ2.
Thickness of both the plates is t.
When both the strips are fitted, the optical path changes by
\[∆ x = \left( \mu_1 - 1 \right) t - \left( \mu_2 - 1 \right) t\]
\[= \left( \mu_1 - \mu_2 \right) t\]
For minimum at P0, the path difference should be \[\frac{\lambda}{2}.\]
i.e. \[∆ x = \frac{\lambda}{2}\]
So, \[\frac{\lambda}{2} = \left( \mu_1 - \mu_2 \right)t\]
\[ \Rightarrow t = \frac{\lambda}{2\left( \mu_1 - \mu_2 \right)}\]
Therefore, minimum at point P0 is \[\frac{\lambda}{2\left( \mu_1 - \mu_2 \right)}.\]
APPEARS IN
संबंधित प्रश्न
In Young’s experiment, the ratio of intensity at the maxima and minima in an interference
pattern is 36 : 9. What will be the ratio of the intensities of two interfering waves?
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
A thin transparent sheet is placed in front of a Young's double slit. The fringe-width will _____________ .
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
A Young's double slit apparatus has slits separated by 0⋅28 mm and a screen 48 cm away from the slits. The whole apparatus is immersed in water and the slits are illuminated by red light \[\left( \lambda = 700\text{ nm in vacuum} \right).\] Find the fringe-width of the pattern formed on the screen.
In a Young's double slit experiment, \[\lambda = 500\text{ nm, d = 1.0 mm and D = 1.0 m.}\] Find the minimum distance from the central maximum for which the intensity is half of the maximum intensity.
Draw a neat labelled diagram of Young’s Double Slit experiment. Show that `beta = (lambdaD)/d` , where the terms have their usual meanings (either for bright or dark fringe).
Wavefront is ______.
Young's double slit experiment is made in a liquid. The 10th bright fringe lies in liquid where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
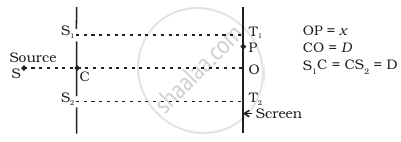
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
In an interference experiment, a third bright fringe is obtained at a point on the screen with a light of 700 nm. What should be the wavelength of the light source in order to obtain the fifth bright fringe at the same point?
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
