Advertisements
Advertisements
प्रश्न
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
उत्तर
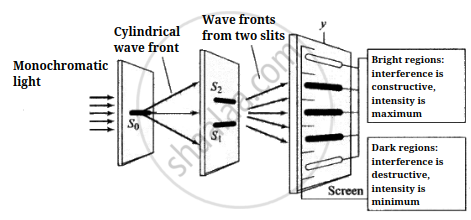
Young's experiment to show interference of light passing through two slits. A pattern of bright and dark areas appears on the screen (as shown in figure (i)).
The condition for destructive interference is `Δx = S_2P - S_1P +- ((2n - 1)/2)lambda` where n = 1, 2, ...
For nth minima to be formed on the screen path difference (Δx) between the rays coming from S1 and S2 must be `((2n - 1)/2)lambda`
The minima will occur when `Δx = S_2P - S_1P = ((2n - 1)/2)lambda` ......(i)
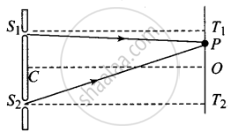
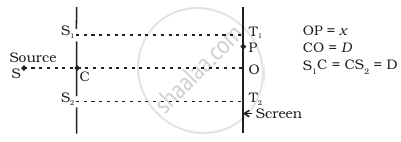
From the given figure,
`S_1P = sqrt((S_1T_1)^2 + (PT_1)^2) = sqrt(D^2 + (D - x)^2)`
And `S_2P = sqrt((S_2T_2)^2 + (T_2P^2)) = sqrt(D^2 + (D + x)^2)`
`T_2P = T_2O + OP = D + x`
And `T_1P = T_1O - OP = D - x`
Hence, `[D^2 + (D + x)^2]^(-1/2) - [D^2 + (D - x)^2]^(1/2) = lambda/2` ......[For first minima n = 1]
If `x = D`
We can write, `[D^2 + 4D^2]^(-1/2) - [D^2 + 0]^(1/2) = lambda/2`
⇒ `[5D^2]^(1/2) - [D^2 + 0]^(1/2) = lambda/2`
⇒ `sqrt(5)D - D = lambda/2` or `D = lambda/(2sqrt(5) - 1)` = 0.404 λ
APPEARS IN
संबंधित प्रश्न
(i) In Young's double-slit experiment, deduce the condition for (a) constructive and (b) destructive interferences at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position 'x' on the screen.
(b) Compare the interference pattern observed in Young's double-slit experiment with single-slit diffraction pattern, pointing out three distinguishing features.
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
Wavefront is ______.
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
