Advertisements
Advertisements
प्रश्न
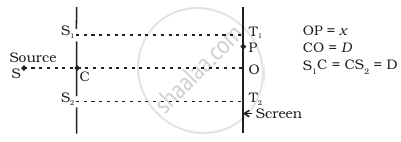
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
उत्तर
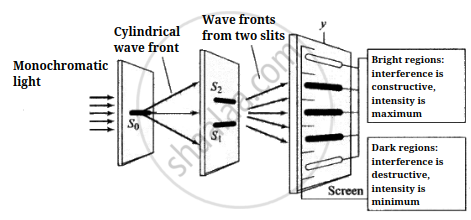
Young's experiment to show interference of light passing through two slits. A pattern of bright and dark areas appears on the screen (as shown in figure (i)).
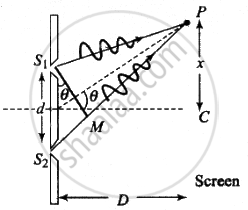
The condition for destructive interference is `Δx = S_2P - S_1P +- ((2n - 1)/2)lambda` where n = 1, 2, ...
For nth minima to be formed on the screen path difference (Δx) between the rays coming from S1 and S2 must be `((2n - 1)/2)lambda`
The minima will occur when `Δx = S_2P - S_1P = ((2n - 1)/2)lambda` ......(i)
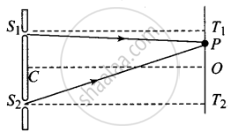
From the given figure,
`S_1P = sqrt((S_1T_1)^2 + (PT_1)^2) = sqrt(D^2 + (D - x)^2)`
And `S_2P = sqrt((S_2T_2)^2 + (T_2P^2)) = sqrt(D^2 + (D + x)^2)`
`T_2P = T_2O + OP = D + x`
And `T_1P = T_1O - OP = D - x`
Hence, `[D^2 + (D + x)^2]^(-1/2) - [D^2 + (D - x)^2]^(1/2) = lambda/2` ......[For first minima n = 1]
If `x = D`
We can write, `[D^2 + 4D^2]^(-1/2) - [D^2 + 0]^(1/2) = lambda/2`
⇒ `[5D^2]^(1/2) - [D^2 + 0]^(1/2) = lambda/2`
⇒ `sqrt(5)D - D = lambda/2` or `D = lambda/(2sqrt(5) - 1)` = 0.404 λ
APPEARS IN
संबंधित प्रश्न
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
The intensity at the central maxima in Young’s double slit experimental set-up is I0. Show that the intensity at a point where the path difference is λ/3 is I0/4.
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
Consider the arrangement shown in the figure. By some mechanism, the separation between the slits S3 and S4 can be changed. The intensity is measured at the point P, which is at the common perpendicular bisector of S1S2 and S2S4. When \[z = \frac{D\lambda}{2d},\] the intensity measured at P is I. Find the intensity when z is equal to

(a) \[\frac{D\lambda}{d}\]
(b) \[\frac{3D\lambda}{2d}\] and
(c) \[\frac{2D\lambda}{d}\]
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
In Young's double slit experiment, show that:
`β = (λ"D")/"d"`
Where the terms have their usual meaning.
