Question

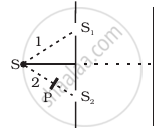
Figure shown a two slit arrangement with a source which emits unpolarised light. P is a polariser with axis whose direction is not given. If I₀ is the intensity of the principal maxima when no polariser is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.

Answer 1

The resultant amplitude of wave reaching the screen will be the sum of amplitude of either wave in perpendicular and parallel polarisation.

Amplitude of the wave in perpendicular polarisation

`A_⊥ = A_⊥^1 + A_⊥^2 = A_⊥^0 sin (kx - ωt) + A_⊥^0 sin (kx - ωt + phi)`

⇒ `A_⊥ = A_⊥^0 (sin (kx - ωt) + sin (kx - ωt + phi)`

Amplitude of the wave in parallel polarisation

`A_(||) = A_(||)^((1)) + A_(||)^((2))`

⇒ `A_(||) = A_(||)^0 [sin (kx - ωt) + sin (kx - ωt + phi)]`

∴ Average Intensity on the screen

`I = {|A_⊥^0|^2 + |A_(||)^0|^2} [sin^2 (kx - ωt)(1 + cos^2 phi + 2 sin phi) + sin^2 (kx - ωt) sin^2 phi]_("average")`

= `{|A_⊥^0|^2 + |A_(||)^0|^2}(1/2)*2(1 + cos phi)`

⇒ `I = 2|A_⊥^0|^2 (1 + cos phi)` since, `|A_⊥^0|_("av") = |A_(||)^0|_("av")`

With polariser P,

Assume `A_⊥^2` is blocked

Intensity = `(A_(||)^1 + A_(||)^2)^2 + (A_⊥^1)^2`

= `|A_⊥^2|^2 (1 + cos phi) + |A_⊥^0|^2 * 1/2`

Given, `I_0 4|A_⊥^0|^2` = Intensity without polariser at principal maxima.

Intensity at first minima with polariser = `|A_⊥^0|^2 (1 - 1) + (|A_⊥^0|^2)/2 = I_0/8`.