Advertisements
Advertisements
प्रश्न
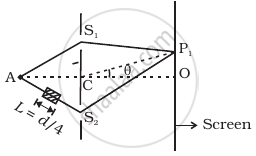
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
उत्तर
When we introduce a thin transparent plate in front of one of the slits in YDSE, the fridge pattern shifts toward the side where the plate is present.
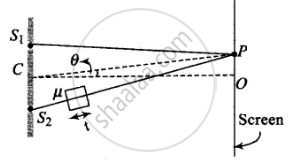
`(S_2O^')_("new") = (S_2O^' - t)_("air") + t_("plate") = (S_2O^' - t)_("air") + mut_("air")`
`(S_2O^')_("new") = S_2O^' + [mu(t - 1)]`
Path difference, `Δx = (S_2O^')_("new") - S_1O^' = (S_2O^' - S_1O^') + [mu(t - 1)]`
⇒ `Δx = d sin theta + [mu(t - 1)]` ......(i)
⇒ Additional path difference = `(mu - 1)t`
Here the separation between the slits = S1S2 = 2d. Hence for calculating path difference, equation (i) becomes `Δx = 2d sin theta + [mu(t - 1)]`
For the principal maxima, (path difference is zero)
`Δx = 2d sin theta_0 + [mu(t - 1)]` = 0
`sin theta_0 = - (L(mu - 1))/(2d) = (-L(0.5))/(2d)` .....[∵ L = d/4]
or ⇒ `sin theta_0 = (-1)/16`
θ0 is the angular position corresponding to the principal maxima
⇒ `OP = D tan theta_0 ≈ D sin theta_0 = (_D)/16`
For the first minima, the path difference is `+- λ/2`
`Δx = 2d sin theta_1 + 0.5 L = +- λ/2`
`sin theta_1 = (+- λ/2 - 0.5 L)/(2d) = (+- λ/2 - d/8)/(2d)`
⇒ `sin theta_1 = (+- λ/2 - λ/8)/(2λ) = +- 1/4 - 1/16` ......[∵ The diffraction occurs if the wavelength of waves is nearly equal to the side width (d)]
On the positive side `sin theta_1^+ = + 1/4 - 1/16 = 3/16`
On the negative side `sin theta_1^- = 1/4 - 1/16 = - 5/16`
The first principal maxima on the positive side is at distance
`D tan theta"'"_1^+ = D (sin theta"'"_1^+)/sqrt(1 - sin^2 theta_1^') = D 3/sqrt(16^2 - 3^2) = (3D)/sqrt(247)` above point O
The first principal minima on the negative side is at distance
`D tan theta_1^+ = (5D)/sqrt(16^2 - 5^2) = (5D)/sqrt(231)` below point O.
APPEARS IN
संबंधित प्रश्न
What is 'diffraction of light'
In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.
Explain why the maxima at `theta=(n+1/2)lambda/a` become weaker and weaker with increasing n
Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10−6 m. The distance between the slit and the screen is 1·5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10−4 m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
The magnifying power of a telescope in normal adjustment is 24, when the length of the telescope tube 1 meter. The focal length of the eye lens is
Diffraction effects are easy to notice in the case of sound waves than in case of light waves because
A polariod (I) is placed in front of a monochromatic source. Another polatiod (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II). Explain.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if orange light is used in place of green light?
Justify your answer.
In a single slit Fraunhofer diffraction experiment, how does the angular width of the central maximum change when the slit width is Increased?
