Advertisements
Advertisements
प्रश्न
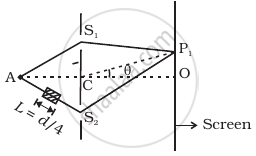
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
Advertisements
उत्तर
When we introduce a thin transparent plate in front of one of the slits in YDSE, the fridge pattern shifts toward the side where the plate is present.
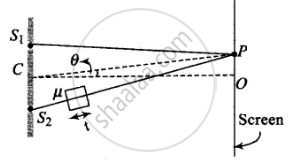
`(S_2O^')_("new") = (S_2O^' - t)_("air") + t_("plate") = (S_2O^' - t)_("air") + mut_("air")`
`(S_2O^')_("new") = S_2O^' + [mu(t - 1)]`
Path difference, `Δx = (S_2O^')_("new") - S_1O^' = (S_2O^' - S_1O^') + [mu(t - 1)]`
⇒ `Δx = d sin theta + [mu(t - 1)]` ......(i)
⇒ Additional path difference = `(mu - 1)t`
Here the separation between the slits = S1S2 = 2d. Hence for calculating path difference, equation (i) becomes `Δx = 2d sin theta + [mu(t - 1)]`
For the principal maxima, (path difference is zero)
`Δx = 2d sin theta_0 + [mu(t - 1)]` = 0
`sin theta_0 = - (L(mu - 1))/(2d) = (-L(0.5))/(2d)` .....[∵ L = d/4]
or ⇒ `sin theta_0 = (-1)/16`
θ0 is the angular position corresponding to the principal maxima
⇒ `OP = D tan theta_0 ≈ D sin theta_0 = (_D)/16`
For the first minima, the path difference is `+- λ/2`
`Δx = 2d sin theta_1 + 0.5 L = +- λ/2`
`sin theta_1 = (+- λ/2 - 0.5 L)/(2d) = (+- λ/2 - d/8)/(2d)`
⇒ `sin theta_1 = (+- λ/2 - λ/8)/(2λ) = +- 1/4 - 1/16` ......[∵ The diffraction occurs if the wavelength of waves is nearly equal to the side width (d)]
On the positive side `sin theta_1^+ = + 1/4 - 1/16 = 3/16`
On the negative side `sin theta_1^- = 1/4 - 1/16 = - 5/16`
The first principal maxima on the positive side is at distance
`D tan theta"'"_1^+ = D (sin theta"'"_1^+)/sqrt(1 - sin^2 theta_1^') = D 3/sqrt(16^2 - 3^2) = (3D)/sqrt(247)` above point O
The first principal minima on the negative side is at distance
`D tan theta_1^+ = (5D)/sqrt(16^2 - 5^2) = (5D)/sqrt(231)` below point O.
APPEARS IN
संबंधित प्रश्न
In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.
In the diffraction pattern due to a single slit of width 'd' with incident light of wavelength 'λ', at an angle of diffraction θ. the condition for first minimum is ....
(a)`lambda sin theta =d`
(b) `d costheta =lambda`
(c)`d sintheta=lambda`
(d) `lambda cos theta=d`
For a single slit of width "a", the first minimum of the interference pattern of a monochromatic light of wavelength λ occurs at an angle of λa. At the same angle of λa, we get a maximum for two narrow slits separated by a distance "a". Explain.
Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10−6 m. The distance between the slit and the screen is 1·5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
Explain two types of diffraction of light.
In Fraunhofer diffraction, how is the angular width of the central bright fringe affected when slit separation is increased?
Show graphically the intensity distribution in Fraunhofer's single slit diffraction experiment. Label the axes.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn to study the diffraction taking place at a single slit of aperture 2 × 10−4m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10−4 m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Monochromatic light of wavelength 4300 Å falls on a slit of width ‘a’. For what value of ‘a’ the first maximum falls at 30° ?
In Fraunhofer diffraction, what kind of a source of light is used and where is it situated?
Which of the following device is used to study the spectra of light?
Write two points of difference between an interference pattern and a diffraction pattern.
How can you differentiate whether a pattern is produced by a single slit or double slit?
Derive the expression for the angular position of (i) bright and (ii) dark fringes produced in a single slit diffraction.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the slit width is decreased?
Justify your answer.
In the diagram shown, the separation between the slit is equal to 3λ, where λ is the wavelength of the light incident on the plane of the slits. A thin film of thickness 3λ and refractive index 2 has been placed in the front of the upper slit. The distance of the central maxima on the screen from O is ______.
Draw a labelled graph showing the variation in intensity of diffracted light with diffracting angle in a single slit Fraunhofer diffraction experiment.
