Advertisements
Advertisements
प्रश्न
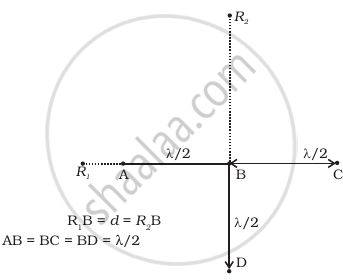
Four identical monochromatic sources A, B, C, D as shown in the (Figure) produce waves of the same wavelength λ and are coherent. Two receiver R1 and R2 are at great but equal distances from B.
- Which of the two receivers picks up the larger signal?
- Which of the two receivers picks up the larger signal when B is turned off?
- Which of the two receivers picks up the larger signal when D is turned off?
- Which of the two receivers can distinguish which of the sources B or D has been turned off?
उत्तर
i. Consider the disturbances at R1 which is a distance d from A. Let the wave at R1 because of A be YA = a cos ωt. The path difference of the signal from A with that from B is λ/2 and hence the phase difference is π.
Thus the wave at R1 because of B is `y_B = a cos (ωt - π) = - a cos ωt)`
The path difference of the signal from C with that from A is λ and hence the phase difference is 2π.
Thus the wave at R1 because of C is yc = a cos ωt.
The path difference between the signal from D with that of A is `sqrt(d^2 + (lambda/2)^2) - (d - lambda/2)`
= `d(1 + lambda/(4d^2))^(1/2) - d + lambda/2`
= `d(1 + lambda^2/(8d^2))^(1/2) - d + lambda/2`
If d >>λ the path difference `∼ λ/2` and hence the phase difference is π.
∴ `y_D = - a cos ωt`
Thus, the signal picked up at R1 is `y_A + y_B + y_C + y_D` = 0
Let the signal picked up at R2 from B be `y_B = a_1 cos ωt`
The path difference between signal at D and that at B is λ/2.
∴ `y_D = - a_1 cos ωt`
The path difference between signal at A and that at B is `sqrt((d)^2 + (lambda/2)^2) - d = d(1 + lambda^2/(4d^2))^(1/2) - d ∼ 1/8 lambda^2/d^2`
∴ The phase difference is `(2pi)/(8λ) * λ^2/d^2 = (piλ)/(4d) = phi ∼ 0`.
Hence, `y_A = a_1 cos (ωt - phi)`
Similarly, `y_C = a_1 cos (ωt - phi)`
∴ Signal picked up by R2 is `y_A + y_B + y_C + y_D = y = 2a_1 cos (ωt - phi)`
∴ `|y|^2 = 4a_1^2 cos^2 (ωt - phi)`
∴ `<I> = 2a_1^2`
Thus R1 picks up the larger signal.
ii. If B is switched off
R1 picks up y = a cos ωt
∴ `<I_(R_1)> = 1/2 a^2`
R2 picks up y = a cos ωt
∴ `<I_(R_2)> = 1/2 a_1^2`
Thus R1 and R2 pick up the same signal.
iii. If D is switched off
R1 picks up y = a cos ω t
∴ `<I_(R_1)> = 1/2 a^2`
R2 picks up y = 3a cos ωt
∴ `<I_(R_2)> = 1/2 9a^2`
Thus R2 picks up a larger signal compared to R1.
iv. Thus a signal at R1 indicates B has been switched off and an enhanced signal at R2 indicates D has been switched off.
APPEARS IN
संबंधित प्रश्न
In the diffraction pattern due to a single slit of width 'd' with incident light of wavelength 'λ', at an angle of diffraction θ. the condition for first minimum is ....
(a)`lambda sin theta =d`
(b) `d costheta =lambda`
(c)`d sintheta=lambda`
(d) `lambda cos theta=d`
Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10−6 m. The distance between the slit and the screen is 1·5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases.
In Fraunhofer diffraction, how is the angular width of the central bright fringe affected when slit separation is increased?
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn to study the diffraction taking place at a single slit of aperture 2 × 10−4m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Monochromatic light of wavelength 4300 Å falls on a slit of width ‘a’. For what value of ‘a’ the first maximum falls at 30° ?
In Fraunhofer diffraction, what kind of a source of light is used and where is it situated?
In a single slit diffraction experiment, how does the angular width of the central maxima change when:
- screen is moved away from the plane of the slit?
- width of the slit is increased?
- light of larger wavelength is used?
Consider the diffraction pattern for a small pinhole. As the size of the hole is increased ______.
- the size decreases.
- the intensity increases.
- the size increases.
- the intensity decreases.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the slit width is decreased?
Justify your answer.
In the diagram shown, the separation between the slit is equal to 3λ, where λ is the wavelength of the light incident on the plane of the slits. A thin film of thickness 3λ and refractive index 2 has been placed in the front of the upper slit. The distance of the central maxima on the screen from O is ______.