Question

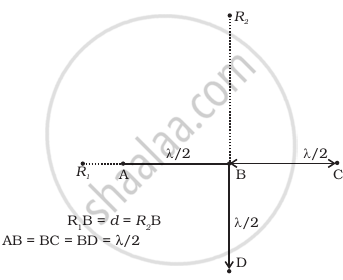
Four identical monochromatic sources A, B, C, D as shown in the (Figure) produce waves of the same wavelength λ and are coherent. Two receiver R₁ and R₂ are at great but equal distances from B.

1. Which of the two receivers picks up the larger signal?
2. Which of the two receivers picks up the larger signal when B is turned off?
3. Which of the two receivers picks up the larger signal when D is turned off?
4. Which of the two receivers can distinguish which of the sources B or D has been turned off?

Answer 1

i. Consider the disturbances at R₁ which is a distance d from A. Let the wave at R₁ because of A be Y_A = a cos ωt. The path difference of the signal from A with that from B is λ/2 and hence the phase difference is π.

Thus the wave at R₁ because of B is `y_B = a cos (ωt - π) = - a cos ωt)`

The path difference of the signal from C with that from A is λ and hence the phase difference is 2π.

Thus the wave at R₁ because of C is y_c = a cos ωt.

The path difference between the signal from D with that of A is `sqrt(d^2 + (lambda/2)^2) - (d - lambda/2)`

= `d(1 + lambda/(4d^2))^(1/2) - d + lambda/2`

= `d(1 + lambda^2/(8d^2))^(1/2) - d + lambda/2`

If d >>λ the path difference `∼ λ/2` and hence the phase difference is π.

∴ `y_D = - a cos ωt`

Thus, the signal picked up at R₁ is `y_A + y_B + y_C + y_D` = 0

Let the signal picked up at R₂ from B be `y_B = a_1 cos ωt`

The path difference between signal at D and that at B is λ/2.

∴  `y_D = - a_1 cos ωt`

The path difference between signal at A and that at B is `sqrt((d)^2 + (lambda/2)^2) - d = d(1 + lambda^2/(4d^2))^(1/2) - d ∼ 1/8 lambda^2/d^2`

∴ The phase difference is `(2pi)/(8λ) * λ^2/d^2 = (piλ)/(4d) = phi ∼ 0`.

Hence, `y_A = a_1 cos (ωt - phi)`

Similarly, `y_C = a_1 cos (ωt - phi)`

∴ Signal picked up by R₂ is `y_A + y_B + y_C + y_D = y = 2a_1 cos (ωt - phi)`

∴ `|y|^2 = 4a_1^2 cos^2 (ωt - phi)`

∴ `<I> = 2a_1^2`

Thus R1 picks up the larger signal.

ii. If B is switched off

R₁ picks up y = a cos ωt

∴ `<I_(R_1)> = 1/2 a^2`

R₂ picks up y = a cos ωt

∴ `<I_(R_2)> = 1/2 a_1^2`

Thus R₁ and R₂ pick up the same signal.

iii. If D is switched off

R₁ picks up y = a cos ω t

∴ `<I_(R_1)> = 1/2 a^2`

R₂ picks up y = 3a cos ωt

∴ `<I_(R_2)> = 1/2 9a^2`

Thus R₂ picks up a larger signal compared to R₁.

iv. Thus a signal at R₁ indicates B has been switched off and an enhanced signal at R₂ indicates D has been switched off.