Advertisements
Advertisements
प्रश्न
Derive the expression for the angular position of (i) bright and (ii) dark fringes produced in a single slit diffraction.
उत्तर
(i) Derivation of expression for the angular position of bright fringe produced by single slit diffraction:
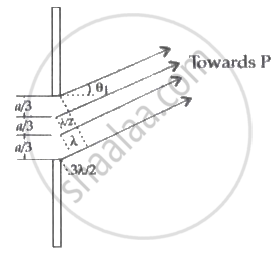
The single slit is now divided into three equal parts.
If waves from two parts of the slit cancel each other, the wave from the third part will produce a maximum at a point between two minimums.
So, sin θ1 = `(3λ)/(2"a")`
Similarly, if the slit is divided into five equal parts, then another maximum will be produced at
sin θ2 = `(5λ)/(2"a")`
Similarly for other fringes, sin θn = `((2"n" + 1)λ)/(2"a")`
Or, θn = `((2"n" + 1)λ)/(2"a")`
For central maximum, θ = 0°
(ii) Derivation of expression for the angular position of dark fringe produced by single slit diffraction:
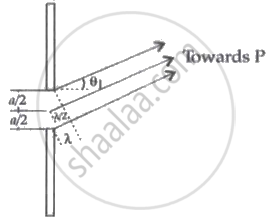
The single slit is divided into two equal halves. Every point in one half has a corresponding point in the other half. The path difference between two waves arriving at point P is
`"a"/(2sinθ_1) = λ/2`
This means the contributions are in opposite phases, so cancel each other and the intensity falls to zero.
So, for 1st dark fringe, sin θ1 = `(λ)/("a")`
Similarly for other dark fringes, sin θn = `("n"λ)/("a")`
θn = `("n"λ)/("a")`
संबंधित प्रश्न
What is 'diffraction of light'
In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.
In the diffraction pattern due to a single slit of width 'd' with incident light of wavelength 'λ', at an angle of diffraction θ. the condition for first minimum is ....
(a)`lambda sin theta =d`
(b) `d costheta =lambda`
(c)`d sintheta=lambda`
(d) `lambda cos theta=d`
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10−4 m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Monochromatic light of wavelength 4300 Å falls on a slit of width ‘a’. For what value of ‘a’ the first maximum falls at 30° ?
In Fraunhofer diffraction, what kind of a source of light is used and where is it situated?
Wavelength of light of frequency 100 Hz is
The magnifying power of a telescope in normal adjustment is 24, when the length of the telescope tube 1 meter. The focal length of the eye lens is
How can you differentiate whether a pattern is produced by a single slit or double slit?
In a single slit Fraunhofer diffraction experiment, how does the angular width of the central maximum change when the slit width is Increased?
