Question

Derive the expression for the angular position of (i) bright and (ii) dark fringes produced in a single slit diffraction.

Answer 1

(i) Derivation of expression for the angular position of bright fringe produced by single slit diffraction:

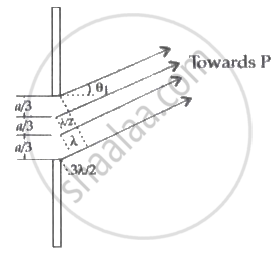
The single slit is now divided into three equal parts.

If waves from two parts of the slit cancel each other, the wave from the third part will produce a maximum at a point between two minimums.

So, sin θ₁ = `(3λ)/(2"a")`

Similarly, if the slit is divided into five equal parts, then another maximum will be produced at

sin θ₂ = `(5λ)/(2"a")`

Similarly for other fringes, sin θ_n = `((2"n" + 1)λ)/(2"a")`

Or, θ_n = `((2"n" + 1)λ)/(2"a")`

For central maximum, θ = 0°

(ii) Derivation of expression for the angular position of dark fringe produced by single slit diffraction:

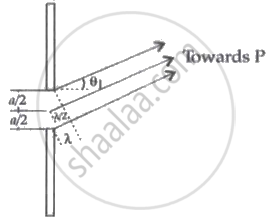
The single slit is divided into two equal halves. Every point in one half has a corresponding point in the other half. The path difference between two waves arriving at point P is

`"a"/(2sinθ_1) = λ/2`

This means the contributions are in opposite phases, so cancel each other and the intensity falls to zero.

So, for 1^st dark fringe, sin θ₁ = `(λ)/("a")`

Similarly for other dark fringes, sin θ_n = `("n"λ)/("a")`

θ_n = `("n"λ)/("a")`