Advertisements
Advertisements
Question
Derive the expression for the angular position of (i) bright and (ii) dark fringes produced in a single slit diffraction.
Solution
(i) Derivation of expression for the angular position of bright fringe produced by single slit diffraction:
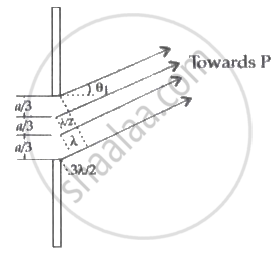
The single slit is now divided into three equal parts.
If waves from two parts of the slit cancel each other, the wave from the third part will produce a maximum at a point between two minimums.
So, sin θ1 = `(3λ)/(2"a")`
Similarly, if the slit is divided into five equal parts, then another maximum will be produced at
sin θ2 = `(5λ)/(2"a")`
Similarly for other fringes, sin θn = `((2"n" + 1)λ)/(2"a")`
Or, θn = `((2"n" + 1)λ)/(2"a")`
For central maximum, θ = 0°
(ii) Derivation of expression for the angular position of dark fringe produced by single slit diffraction:
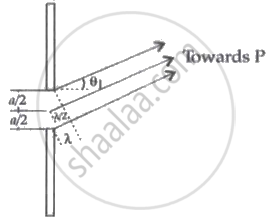
The single slit is divided into two equal halves. Every point in one half has a corresponding point in the other half. The path difference between two waves arriving at point P is
`"a"/(2sinθ_1) = λ/2`
This means the contributions are in opposite phases, so cancel each other and the intensity falls to zero.
So, for 1st dark fringe, sin θ1 = `(λ)/("a")`
Similarly for other dark fringes, sin θn = `("n"λ)/("a")`
θn = `("n"λ)/("a")`
RELATED QUESTIONS
A point is situated at 7cm and 7·2 cm from two coherent sources. Find the· nature of illumination at the point if wavelength of light is 4000A.
In Fraunhofer diffraction, how is the angular width of the central bright fringe affected when slit separation is increased?
Draw the intensity distribution for the diffraction bands produced due to single slit ?
Wavelength of light of frequency 100 Hz is
Direction of the first secondary maximum in the Fraunhoffer diffraction pattern at a single slit is given by (a is the width of the slit):
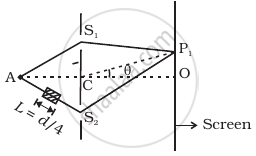
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through a single slit. What is the width of the central maximum in comparison to that of a secondary maximum?
Write two points of difference between an interference pattern and a diffraction pattern.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the screen is moved closer to the slit?
Justify your answer.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the slit width is decreased?
Justify your answer.
