Advertisements
Advertisements
Question
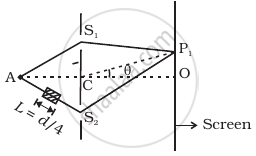
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
Advertisements
Solution
When we introduce a thin transparent plate in front of one of the slits in YDSE, the fridge pattern shifts toward the side where the plate is present.
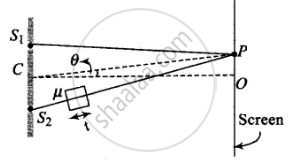
`(S_2O^')_("new") = (S_2O^' - t)_("air") + t_("plate") = (S_2O^' - t)_("air") + mut_("air")`
`(S_2O^')_("new") = S_2O^' + [mu(t - 1)]`
Path difference, `Δx = (S_2O^')_("new") - S_1O^' = (S_2O^' - S_1O^') + [mu(t - 1)]`
⇒ `Δx = d sin theta + [mu(t - 1)]` ......(i)
⇒ Additional path difference = `(mu - 1)t`
Here the separation between the slits = S1S2 = 2d. Hence for calculating path difference, equation (i) becomes `Δx = 2d sin theta + [mu(t - 1)]`
For the principal maxima, (path difference is zero)
`Δx = 2d sin theta_0 + [mu(t - 1)]` = 0
`sin theta_0 = - (L(mu - 1))/(2d) = (-L(0.5))/(2d)` .....[∵ L = d/4]
or ⇒ `sin theta_0 = (-1)/16`
θ0 is the angular position corresponding to the principal maxima
⇒ `OP = D tan theta_0 ≈ D sin theta_0 = (_D)/16`
For the first minima, the path difference is `+- λ/2`
`Δx = 2d sin theta_1 + 0.5 L = +- λ/2`
`sin theta_1 = (+- λ/2 - 0.5 L)/(2d) = (+- λ/2 - d/8)/(2d)`
⇒ `sin theta_1 = (+- λ/2 - λ/8)/(2λ) = +- 1/4 - 1/16` ......[∵ The diffraction occurs if the wavelength of waves is nearly equal to the side width (d)]
On the positive side `sin theta_1^+ = + 1/4 - 1/16 = 3/16`
On the negative side `sin theta_1^- = 1/4 - 1/16 = - 5/16`
The first principal maxima on the positive side is at distance
`D tan theta"'"_1^+ = D (sin theta"'"_1^+)/sqrt(1 - sin^2 theta_1^') = D 3/sqrt(16^2 - 3^2) = (3D)/sqrt(247)` above point O
The first principal minima on the negative side is at distance
`D tan theta_1^+ = (5D)/sqrt(16^2 - 5^2) = (5D)/sqrt(231)` below point O.
APPEARS IN
RELATED QUESTIONS
A point is situated at 7cm and 7·2 cm from two coherent sources. Find the· nature of illumination at the point if wavelength of light is 4000A.
Explain why the maxima at `theta=(n+1/2)lambda/a` become weaker and weaker with increasing n
For a single slit of width "a", the first minimum of the interference pattern of a monochromatic light of wavelength λ occurs at an angle of λa. At the same angle of λa, we get a maximum for two narrow slits separated by a distance "a". Explain.
Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
Explain two types of diffraction of light.
In Fraunhofer diffraction, how is the angular width of the central bright fringe affected when slit separation is increased?
Show graphically the intensity distribution in Fraunhofer's single slit diffraction experiment. Label the axes.
In Fraunhofer diffraction, what kind of a source of light is used and where is it situated?
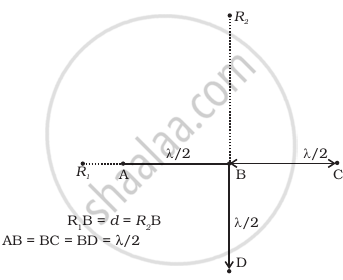
Four identical monochromatic sources A, B, C, D as shown in the (Figure) produce waves of the same wavelength λ and are coherent. Two receiver R1 and R2 are at great but equal distances from B.
- Which of the two receivers picks up the larger signal?
- Which of the two receivers picks up the larger signal when B is turned off?
- Which of the two receivers picks up the larger signal when D is turned off?
- Which of the two receivers can distinguish which of the sources B or D has been turned off?
Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through a single slit. What is the width of the central maximum in comparison to that of a secondary maximum?
How can you differentiate whether a pattern is produced by a single slit or double slit?
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if orange light is used in place of green light?
Justify your answer.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the screen is moved closer to the slit?
Justify your answer.
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the slit width is decreased?
Justify your answer.
In the diagram shown, the separation between the slit is equal to 3λ, where λ is the wavelength of the light incident on the plane of the slits. A thin film of thickness 3λ and refractive index 2 has been placed in the front of the upper slit. The distance of the central maxima on the screen from O is ______.
Draw a labelled graph showing the variation in intensity of diffracted light with diffracting angle in a single slit Fraunhofer diffraction experiment.
