Advertisements
Advertisements
Question
Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
Advertisements
Solution
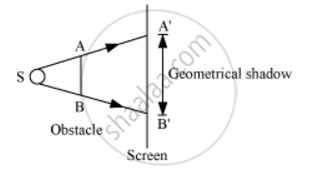
The phenomenon of bending of light round the sharp corners of an obstacle and spreading into the regions of the geometrical shadow is called diffraction.
Expression For Fringe Width
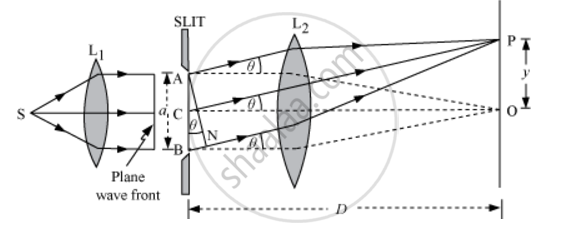
Consider a parallel beam of light from a lens falling on a slit AB. As diffraction occurs, the pattern is focused on the screen XY with the help of lens L2. We will obtain a diffraction pattern that is a central maximum at the centre O flanked by a number of dark and bright fringes called secondary maxima and minima.
Central Maximum − Each point on the plane wave front AB sends out secondary wavelets in all directions. The waves from points equidistant from the centre C lying on the upper and lower half reach point O with zero path difference and hence, reinforce each other, producing maximum intensity at point O.
Positions and Widths of Secondary Maxima and Minima
Consider a point P on the screen at which wavelets travelling in a direction making angle θ with CO are brought to focus by the lens. The wavelets from points A and B will have a path difference equal to BN.
From the right-angled ΔANB, we have:
BN = AB sinθ
BN = a sinθ …(i)
Suppose BN = λ and θ = θ1
Then, the above equation gives
λ = a sin θ1
`sintheta_1=lambda/a`
Such a point on the screen will be the position of first secondary minimum
If BN = 2λ and θ= θ2, then
2λ = a sin θ2
`sin_2=(2lambda)/a `
Such a point on the screen will be the position of second secondary minimum.
In general, for nth minimum at point P,
`sintheta_n=(nlambda)/a`
If yn is the distance of the nth minimum from the centre of the screen, from right-angled ΔCOP, we have:
`tantheta_n=(OP)/(CO)`
`tantheta_n=y_n/D`
In case θn is small, sin θn ≈ tan θn
∴ Equations (iv) and (v) give
`y_n/D=(nlambda)/a`
`y_n=(nDlambda)/a`
Width of the secondary maximum,
`beta=y_n-y_(n-1)=(nDlambda)/a-((n-1)Dlambda)/a`
`beta=(Dlambda)/a ...(vi)`
∴ β is independent of n, all the secondary maxima are of the same width β.
If `BN=(3lambda)/2`and `theta=theta_1^'`, from equation (i), we have:
`sin_1^'=(3lambda)/(2a)`
Such a point on the screen will be the position of the first secondary maximum.
Corresponding to path difference,
`BN=(5lambda)/2`and `theta=theta_2^'`the second secondary maximum is produced
In general, for the nth maximum at point P,
`sin_n^'=((2n+1)lambda)/(2a) `
If `y_n^'`is the distance of nth maximum from the centre of the screen, then the angular position of the nth maximum is given by
`tantheta_n^'=y_n^'/D `
In case `theta_n^'`is small
`sintheta_n^' ~~tantheta_n^'`
`:.y_n^'=((2n+1)Dlambda)/(2a)`
Width of the secondary minimum,
β' = y'n − y'n−1 = `(nDlambda)/a-((n-1)Dlambda)/a`
`beta'=(Dlambda)/a `
Since β' is independent of n, all the secondary minima are of the same width β'
APPEARS IN
RELATED QUESTIONS
In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn to study the diffraction taking place at a single slit of aperture 2 × 10−4m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10−4 m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Monochromatic light of wavelength 4300 Å falls on a slit of width ‘a’. For what value of ‘a’ the first maximum falls at 30° ?
Direction of the first secondary maximum in the Fraunhoffer diffraction pattern at a single slit is given by (a is the width of the slit):
Which of the following device is used to study the spectra of light?
Consider the diffraction pattern for a small pinhole. As the size of the hole is increased ______.
- the size decreases.
- the intensity increases.
- the size increases.
- the intensity decreases.
A polariod (I) is placed in front of a monochromatic source. Another polatiod (II) is placed in front of this polaroid (I) and rotated till no light passes. A third polaroid (III) is now placed in between (I) and (II). In this case, will light emerge from (II). Explain.
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
In the diagram shown, the separation between the slit is equal to 3λ, where λ is the wavelength of the light incident on the plane of the slits. A thin film of thickness 3λ and refractive index 2 has been placed in the front of the upper slit. The distance of the central maxima on the screen from O is ______.
