Advertisements
Advertisements
Question
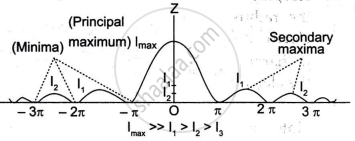
Draw a labelled graph showing the variation in intensity of diffracted light with diffracting angle in a single slit Fraunhofer diffraction experiment.
Solution
Intensity distribution for Fraunhofer diffraction at a single slit.
APPEARS IN
RELATED QUESTIONS
What is 'diffraction of light'
A point is situated at 7cm and 7·2 cm from two coherent sources. Find the· nature of illumination at the point if wavelength of light is 4000A.
In Fraunhofer diffraction, how is the angular width of the central bright fringe affected when slit separation is increased?
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn to study the diffraction taking place at a single slit of aperture 2 × 10−4m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10−4 m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases.
Monochromatic light of wavelength 4300 Å falls on a slit of width ‘a’. For what value of ‘a’ the first maximum falls at 30° ?
The penetration of light into the region of geomaterial shadow is called.
Direction of the first secondary maximum in the Fraunhoffer diffraction pattern at a single slit is given by (a is the width of the slit):
Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through a single slit. What is the width of the central maximum in comparison to that of a secondary maximum?
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the screen is moved closer to the slit?
Justify your answer.
