Advertisements
Advertisements
Question
In a diffraction pattern due to a single slit, how will the angular width of the central maximum change, if the screen is moved closer to the slit?
Justify your answer.
Solution
The angular width of central maxima of a single slit diffraction pattern is 2θ = `(2λ)/"a"`
Angular width of the central maxima is independent of the distance between the slit and the screen. So, if the screen is moved closer to the slit there will be no change in the angular width of the central maxima.
APPEARS IN
RELATED QUESTIONS
In a single slit diffraction pattern, the distance between first minima on the right and first minima on the left of central maximum is 4 mm. The screen on which the pattern is displaced, is 2m from the slit and wavelength of light used is 6000Å. Calculate width of the slit and width of the central maximum.
In the diffraction pattern due to a single slit of width 'd' with incident light of wavelength 'λ', at an angle of diffraction θ. the condition for first minimum is ....
(a)`lambda sin theta =d`
(b) `d costheta =lambda`
(c)`d sintheta=lambda`
(d) `lambda cos theta=d`
Show graphically the intensity distribution in Fraunhofer's single slit diffraction experiment. Label the axes.
Draw the intensity distribution for the diffraction bands produced due to single slit ?
The penetration of light into the region of geomaterial shadow is called.
Direction of the first secondary maximum in the Fraunhoffer diffraction pattern at a single slit is given by (a is the width of the slit):
Which of the following device is used to study the spectra of light?
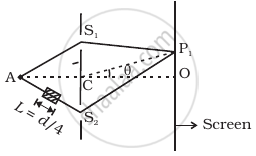
AC = CO = D, S1C = S2C = d << D
A small transparent slab containing material of µ = 1.5 is placed along AS2 (Figure). What will be the distance from O of the principal maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab?
Draw the graph showing intensity distribution of fringes with phase angle due to diffraction through a single slit. What is the width of the central maximum in comparison to that of a secondary maximum?
In a single slit Fraunhofer diffraction experiment, how does the angular width of the central maximum change when the slit width is Increased?
