Advertisements
Advertisements
प्रश्न
Figure shown a two slit arrangement with a source which emits unpolarised light. P is a polariser with axis whose direction is not given. If I0 is the intensity of the principal maxima when no polariser is present, calculate in the present case, the intensity of the principal maxima as well as of the first minima.
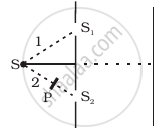
उत्तर
The resultant amplitude of wave reaching the screen will be the sum of amplitude of either wave in perpendicular and parallel polarisation.
Amplitude of the wave in perpendicular polarisation
`A_⊥ = A_⊥^1 + A_⊥^2 = A_⊥^0 sin (kx - ωt) + A_⊥^0 sin (kx - ωt + phi)`
⇒ `A_⊥ = A_⊥^0 (sin (kx - ωt) + sin (kx - ωt + phi)`
Amplitude of the wave in parallel polarisation
`A_(||) = A_(||)^((1)) + A_(||)^((2))`
⇒ `A_(||) = A_(||)^0 [sin (kx - ωt) + sin (kx - ωt + phi)]`
∴ Average Intensity on the screen
`I = {|A_⊥^0|^2 + |A_(||)^0|^2} [sin^2 (kx - ωt)(1 + cos^2 phi + 2 sin phi) + sin^2 (kx - ωt) sin^2 phi]_("average")`
= `{|A_⊥^0|^2 + |A_(||)^0|^2}(1/2)*2(1 + cos phi)`
⇒ `I = 2|A_⊥^0|^2 (1 + cos phi)` since, `|A_⊥^0|_("av") = |A_(||)^0|_("av")`
With polariser P,
Assume `A_⊥^2` is blocked
Intensity = `(A_(||)^1 + A_(||)^2)^2 + (A_⊥^1)^2`
= `|A_⊥^2|^2 (1 + cos phi) + |A_⊥^0|^2 * 1/2`
Given, `I_0 4|A_⊥^0|^2` = Intensity without polariser at principal maxima.
Intensity at first minima with polariser = `|A_⊥^0|^2 (1 - 1) + (|A_⊥^0|^2)/2 = I_0/8`.
APPEARS IN
संबंधित प्रश्न
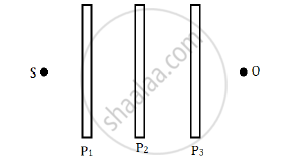
Three identical polaroid sheets P1, P2 and P3 are oriented so that the pass axis of P2 and P3 are inclined at angles of 60° and 90° respectively with the pass axis of P1. A monochromatic source S of unpolarised light of intensity I0 is kept in front of the polaroid sheet P1 as shown in the figure. Determine the intensities of light as observed by the observer at O, when polaroid P3 is rotated with respect to P2 at angles θ = 30° and 60°.
Show, with the help of a diagram, how unpolarised sunlight gets polarised due to scattering.
When a low flying aircraft passes overhead, we sometimes notice a slight shaking of the picture on our TV screen. Suggest a possible explanation.
A ray of light passes from a vacuum to a medium of refractive index (μ). The angle of
incidence is found to be twice the angle of refraction. The angle of incidence is _______.
A) `cos^(-1)(mu/2)`
B) cos−1(μ)
C) `2 cos^(-1) (mu/2)`
D) `2 sin^(-1) (mu/2)`
The glass plate of refractive index 1.732 is to be used as a polarizer, its polarising angle is _______.
With the help of an experiment, state how will you identify whether a given beam of light is polarised or unpolarized?
Explain how an unpolarised light gets polarised when incident on the interface separating the two transparent media.
Discuss polarisation by selective absorption.
What is plane polarised light?
How is polarisation of light obtained by scattering of light?
