Advertisements
Advertisements
प्रश्न
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
Advertisements
उत्तर
Diagrammatical arrangement for Young’s double slit experiment:
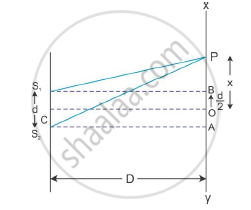
In the above figure, S1 and S2 are two narrow closely spaced slits illuminated by monochromatic light of wavelength λ. The screen on which the interference pattern is observed is represented as XY.
If S1 and S2 emit light in the same phase, then for point O, the path difference receives light in the same phase. The superposition at O is constructive producing a bright point called the central maxima. The intensity at any point P at a distance x from O depends on the path difference between light reaching P from S1 and S2. The path difference is S2P − S1P.
From the geometry of the figure, we have
`(S_2P)^2=D^2+(x+d/2)^2`
Similarly, we have
`(S_1P)^2=D^2+(x+d/2)^2`
`:.(S_2P)^2-(S_1P)^2=D^2+(x+d/2)^2-D^2-(x-d/2)^2`
`:.(S_2P)^2-(S_1P)^2=(x+d/2)^2-(x-d/2)^2`
`:.(S_2P)^2-(S_1P)^2=x^2+xd+d^2/4-x^2+xd-d^2/4`
∴ (S2P)2-(S1P)2=2xd
∴(S2P-S1P)(S2P+S1P)=2xd
`:.S_2P-S_1P=(2xd)/(S_2P+S_1P)`
Now, from the figure we can see that
S2P≈S1P = D
`:.S_2P-S_1P=(2xd)/(2D)=(xd)/D`
This is the expression for path difference.
Condition for constructive interference: Constructive interference will occur when the phase difference between the two superposing waves is an even multiple of π or the path difference is an integral multiple of wavelength λ.
Condition for destructive interference: Destructive interference will occur when the phase difference between the two superposing waves is an odd multiple of π or the path difference is an odd multiple of wavelength λ/2.
संबंधित प्रश्न
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
In a Young’s double-slit experiment, the slits are separated by 0.28 mm and the screen is placed 1.4 m away. The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm. Determine the wavelength of light used in the experiment.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
The intensity at the central maxima in Young’s double slit experimental set-up is I0. Show that the intensity at a point where the path difference is λ/3 is I0/4.
A Young's double slit experiment is performed with white light.
(a) The central fringe will be white.
(b) There will not be a completely dark fringe.
(c) The fringe next to the central will be red.
(d) The fringe next to the central will be violet.
In a Young's double slit experiment, two narrow vertical slits placed 0.800 mm apart are illuminated by the same source of yellow light of wavelength 589 nm. How far are the adjacent bright bands in the interference pattern observed on a screen 2.00 m away?
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
A source emitting light of wavelengths 480 nm and 600 nm is used in a double-slit interference experiment. The separation between the slits is 0.25 mm and the interference is observed on a screen placed at 150 cm from the slits. Find the linear separation between the first maximum (next to the central maximum) corresponding to the two wavelengths.
White light is used in a Young's double slit experiment. Find the minimum order of the violet fringe \[\left( \lambda = 400\text{ nm} \right)\] which overlaps with a red fringe \[\left( \lambda = 700\text{ nm} \right).\]
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A mica strip and a polystyrene strip are fitted on the two slits of a double slit apparatus. The thickness of the strips is 0.50 mm and the separation between the slits is 0.12 cm. The refractive index of mica and polystyrene are 1.58 and 1.55, respectively, for the light of wavelength 590 nm which is used in the experiment. The interference is observed on a screen at a distance one metre away. (a) What would be the fringe-width? (b) At what distance from the centre will the first maximum be located?
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
What should be the path difference between two waves reaching a point for obtaining constructive interference in Young’s Double Slit experiment ?
Wavefront is ______.
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
In Young's double slit experiment the slits are 0.589 mm apart and the interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 7.5 mm from the dark fringe which is second from the center of the fringe pattern. Find the wavelength of the light used.
Two balls are projected at an angle θ and (90° − θ) to the horizontal with the same speed. The ratio of their maximum vertical heights is:
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
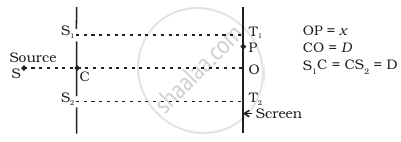
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
A beam of light consisting of two wavelengths 600 nm and 500 nm is used in Young's double slit experiment. The silt separation is 1.0 mm and the screen is kept 0.60 m away from the plane of the slits. Calculate:
- the distance of the second bright fringe from the central maximum for wavelength 500 nm, and
- the least distance from the central maximum where the bright fringes due to both wavelengths coincide.
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
In a Young's double slit experiment, the width of the one of the slit is three times the other slit. The amplitude of the light coming from a slit is proportional to the slit- width. Find the ratio of the maximum to the minimum intensity in the interference pattern.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
