Advertisements
Advertisements
प्रश्न
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
उत्तर
Young’s double slit experiment: Consider two narrow rectangular slits S1 and S2 placed perpendicular to the plane of paper. Slit S is placed on the perpendicular bisector of S1S2 and is illuminated with monochromatic light.
The slits are separated by a small distance d. A screen is placed at a distance D from S1, S2.
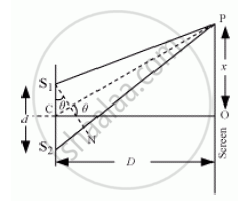
Consider a point P on the screen at distance x from O.
The path difference between the waves reaching P from S1 and S2 is:
P = S2P − S1P
Draw S1N perpendicular to S2P. Then,
P = S2P − S1P = S2P − NP = S2N
From right-angled
`DeltaS_1S^2N=(S_2N)/(S_2S_1) = sintheta`
`therefore P =S_2N=S_2S_1sintheta = d sintheta`
From ΔCOP,
When θ is small,
`sintheta≈theta≈tantheta = x/D`
`therefore P=(xd)/D`
For constructive interference,
`(xd)/D =nlambda,n=0,1,2,3,.....`
Position of nth bright fringe, `x_n = (nDlambda)/d =0,(Dlambda)/d,(2Dlambda)/d,(3Dlambda)/d,.......`
When n = 0, xn = 0, central bright fringe is formed at O.
For destructive interference,
`(xd)/D = (2n +1)lambda/2`
`or x_n = (2_n +1) (lambdaD)/(2d) = 1/2(lambdaD)/d,3/2(lambdaD)/d,5/2(lambdaD)/d,......`
Thus, alternate bright and dark fringes are formed on the screen.
संबंधित प्रश्न
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
The ratio of the intensities at minima to the maxima in the Young's double slit experiment is 9 : 25. Find the ratio of the widths of the two slits.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
