Advertisements
Advertisements
प्रश्न
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
Advertisements
उत्तर
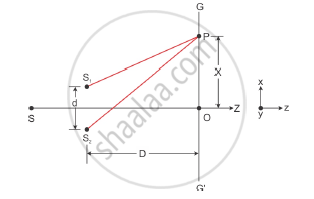
Young’s double slit experiment demonstrated the phenomenon of interference of light. Consider two fine slits S1 and S2 at a small distance d apart. Let the slits be illuminated by a monochromatic source of light of wavelength λ. Let GG′ be a screen kept at a distance D from the slits. The two waves emanating from slits S1 and S2 superimpose on each other resulting in the formation of an interference pattern on the screen placed parallel to the slits.
Let O be the centre of the distance between the slits. The intensity of light at a point on the screen will depend on the path difference between the two waves reaching that point. Consider an arbitrary point P at a distance x from O on the screen.
Path difference between two waves at P = S2P − S1P
The intensity at the point P is maximum or minimum as the path difference is an integral multiple of wavelength or an odd integral multiple of half wavelength
For the point P to correspond to maxima, we must have
S2P − S1P = n, n = 0, 1, 2, 3...
From the figure given above
`(S_2P)^2-(S_1P)^2=D^2+(x+d/2)^2-D^2+(x-d/2)^2`
On solving we get:
(S2P)2-(S1P)2=2xd
`S_2P-S_1P=(2xd)/(S_2P+S_1P)`
As d<<D, then S2P + S2P = 2D (∵ S1P = S2P ≡ D when d<<D)
`:.S_2P-S_1P=(2xd)/(2D)=(xd)/D`
Path difference, `S_2P-S_1P=(xd)/D`
Hence, when constructive interfernce occur, bright region is formed.
For maxima or bright fringe, path difference = `xd/D=nlambda`
i.e `x=(nlambdaD)/d`
where n=0,± 1, ±2,........
During destructive interference, dark fringes are formed:
Path difference, `(xd)/D=(n+1/2)lambda`
`x=(n+1/2)(lambdaD)/d`
The dark fringe and the bright fringe are equally spaced and the distance between consecutive bright and dark fringe is given by:
β = xn+1-xn
`beta=((n+1)lambdaD)/d-(nlambdaD)/d`
`beta=(lambdaD)/d`
Hence the fringe width is given by `beta = (lambdaD)/d`
APPEARS IN
संबंधित प्रश्न
Derive an expression for path difference in Young’s double slit experiment and obtain the conditions for constructive and destructive interference at a point on the screen.
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
Find the angular separation between the consecutive bright fringes in a Young's double slit experiment with blue-green light of wavelength 500 nm. The separation between the slits is \[2 \cdot 0 \times {10}^{- 3}m.\]
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
In a Young's double slit experiment, the separation between the slits = 2.0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2.0 m. If the intensity at the centre of the central maximum is 0.20 W m−2, what will be the intensity at a point 0.5 cm away from this centre along the width of the fringes?
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
How will the interference pattern in Young's double-slit experiment be affected if the phase difference between the light waves emanating from the two slits S1 and S2 changes from 0 to π and remains constant?
In Young's double slit experiment using light of wavelength 600 nm, the slit separation is 0.8 mm and the screen is kept 1.6 m from the plane of the slits. Calculate
- the fringe width
- the distance of (a) third minimum and (b) fifth maximum, from the central maximum.
In Young’s double slit experiment, how is interference pattern affected when the following changes are made:
- Slits are brought closer to each other.
- Screen is moved away from the slits.
- Red coloured light is replaced with blue coloured light.
