Advertisements
Advertisements
प्रश्न
Derive the expression for the magnetic field due to a solenoid of length ‘2l’, radius ‘a’ having ’n’ number of turns per unit length and carrying a steady current ‘I’ at a point
on the axial line, distance ‘r’ from the centre of the solenoid. How does this expression compare with the axial magnetic field due to a bar magnet of magnetic moment ‘m’?
उत्तर
Consider a solenoid of length 2l, radius a and having n turns per unit length. It is carrying a current I.
We have to evaluate the axial field at a point P at a distance r from the centre of the solenoid

Consider a circular element of thickness dx of the solenoid at a distance x from its centre.
The magnitude of the field due to this circular loop carrying a current I is given as
`dB=(mu_0dxnIa^2)/(2[(r-x)^2+a^2]^(3/2))`
The magnitude of the total field is obtained by integrating over all the elements from x = −l to x = +l.
`B=(mu_0nIa^2)/2int_(-1)^(+1)dx/(2[(r-x)^2+a^2]^(3/2))`
Consider the far axial field of the solenoid, so r ≫a and r≫l. Hence, we have
[(r-x)2+a2]3/2 ≈ r3
So, we get
`B=(mu_0nIa^2)/(2r^3)int_(-1)^(+1)dx`
`B=(mu_0nIa^2)/(2r^3)2l`
The magnitude of the magnetic moment of the solenoid is
m Total number of turns current cross-sectional area
m=(nx2l)xIx(πa2)
Therefore, we get the magnetic field as
`B=(mu_0)/(4pi) (2m)/r^3`
This is the expression for magnetic field due to a solenoid on the axial line at a distance r from the centre.
This magnetic field is also the field due to a bar magnet of magnetic moment m.
APPEARS IN
संबंधित प्रश्न
Obtain an expression for the energy stored in a solenoid of self-inductance ‘L’ when the current through it grows from zero to ‘I’.
Two long coaxial insulated solenoids, S1 and S2 of equal lengths are wound one over the other as shown in the figure. A steady current "I" flow thought the inner solenoid S1 to the other end B, which is connected to the outer solenoid S2 through which the same current "I" flows in the opposite direction so as to come out at end A. If n1 and n2 are the number of turns per unit length, find the magnitude and direction of the net magnetic field at a point (i) inside on the axis and (ii) outside the combined system
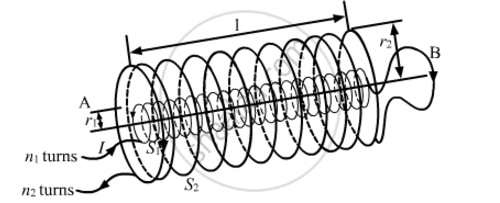
Obtain the expression for mutual inductance of a pair of long coaxial solenoids each of length l and radii r1 and r2 (r2 >> r1). Total number of turns in the two solenoids are N1 and N2, respectively.
A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.
Define self-inductance of a coil.
A wire AB is carrying a steady current of 6 A and is lying on the table. Another wire CD carrying 4 A is held directly above AB at a height of 1 mm. Find the mass per unit length of the wire CD so that it remains suspended at its position when left free. Give the direction of the current flowing in CD with respect to that in AB. [Take the value of g = 10 ms−2]
A long solenoid of radius 2 cm has 100 turns/cm and carries a current of 5 A. A coil of radius 1 cm having 100 turns and a total resistance of 20 Ω is placed inside the solenoid coaxially. The coil is connected to a galvanometer. If the current in the solenoid is reversed in direction, find the charge flown through the galvanometer.
A copper wire having resistance 0.01 ohm in each metre is used to wind a 400-turn solenoid of radius 1.0 cm and length 20 cm. Find the emf of a battery which when connected across the solenoid will cause a magnetic field of 1.0 × 10−2 T near the centre of the solenoid.
A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of magnetic field will be equal to ______.
