Advertisements
Advertisements
प्रश्न
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
Advertisements
उत्तर
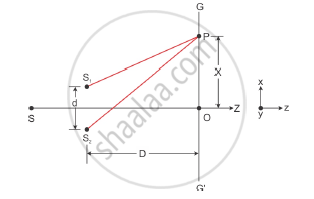
Young’s double slit experiment demonstrated the phenomenon of interference of light. Consider two fine slits S1 and S2 at a small distance d apart. Let the slits be illuminated by a monochromatic source of light of wavelength λ. Let GG′ be a screen kept at a distance D from the slits. The two waves emanating from slits S1 and S2 superimpose on each other resulting in the formation of an interference pattern on the screen placed parallel to the slits.
Let O be the centre of the distance between the slits. The intensity of light at a point on the screen will depend on the path difference between the two waves reaching that point. Consider an arbitrary point P at a distance x from O on the screen.
Path difference between two waves at P = S2P − S1P
The intensity at the point P is maximum or minimum as the path difference is an integral multiple of wavelength or an odd integral multiple of half wavelength
For the point P to correspond to maxima, we must have
S2P − S1P = n, n = 0, 1, 2, 3...
From the figure given above
`(S_2P)^2-(S_1P)^2=D^2+(x+d/2)^2-D^2+(x-d/2)^2`
On solving we get:
(S2P)2-(S1P)2=2xd
`S_2P-S_1P=(2xd)/(S_2P+S_1P)`
As d<<D, then S2P + S2P = 2D (∵ S1P = S2P ≡ D when d<<D)
`:.S_2P-S_1P=(2xd)/(2D)=(xd)/D`
Path difference, `S_2P-S_1P=(xd)/D`
Hence, when constructive interfernce occur, bright region is formed.
For maxima or bright fringe, path difference = `xd/D=nlambda`
i.e `x=(nlambdaD)/d`
where n=0,± 1, ±2,........
During destructive interference, dark fringes are formed:
Path difference, `(xd)/D=(n+1/2)lambda`
`x=(n+1/2)(lambdaD)/d`
The dark fringe and the bright fringe are equally spaced and the distance between consecutive bright and dark fringe is given by:
β = xn+1-xn
`beta=((n+1)lambdaD)/d-(nlambdaD)/d`
`beta=(lambdaD)/d`
Hence the fringe width is given by `beta = (lambdaD)/d`
APPEARS IN
संबंधित प्रश्न
What is the effect on the fringe width if the distance between the slits is reduced keeping other parameters same?
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
Write the conditions on path difference under which constructive interference occurs in Young’s double-slit experiment.
In a Young’s double slit experiment, the source is white light. One of the holes is covered by a red filter and another by a blue filter. In this case ______.
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
