Advertisements
Advertisements
Question
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
Advertisements
Solution
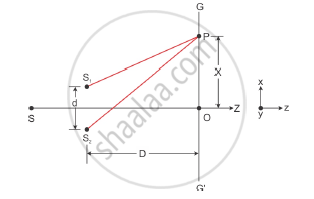
Young’s double slit experiment demonstrated the phenomenon of interference of light. Consider two fine slits S1 and S2 at a small distance d apart. Let the slits be illuminated by a monochromatic source of light of wavelength λ. Let GG′ be a screen kept at a distance D from the slits. The two waves emanating from slits S1 and S2 superimpose on each other resulting in the formation of an interference pattern on the screen placed parallel to the slits.
Let O be the centre of the distance between the slits. The intensity of light at a point on the screen will depend on the path difference between the two waves reaching that point. Consider an arbitrary point P at a distance x from O on the screen.
Path difference between two waves at P = S2P − S1P
The intensity at the point P is maximum or minimum as the path difference is an integral multiple of wavelength or an odd integral multiple of half wavelength
For the point P to correspond to maxima, we must have
S2P − S1P = n, n = 0, 1, 2, 3...
From the figure given above
`(S_2P)^2-(S_1P)^2=D^2+(x+d/2)^2-D^2+(x-d/2)^2`
On solving we get:
(S2P)2-(S1P)2=2xd
`S_2P-S_1P=(2xd)/(S_2P+S_1P)`
As d<<D, then S2P + S2P = 2D (∵ S1P = S2P ≡ D when d<<D)
`:.S_2P-S_1P=(2xd)/(2D)=(xd)/D`
Path difference, `S_2P-S_1P=(xd)/D`
Hence, when constructive interfernce occur, bright region is formed.
For maxima or bright fringe, path difference = `xd/D=nlambda`
i.e `x=(nlambdaD)/d`
where n=0,± 1, ±2,........
During destructive interference, dark fringes are formed:
Path difference, `(xd)/D=(n+1/2)lambda`
`x=(n+1/2)(lambdaD)/d`
The dark fringe and the bright fringe are equally spaced and the distance between consecutive bright and dark fringe is given by:
β = xn+1-xn
`beta=((n+1)lambdaD)/d-(nlambdaD)/d`
`beta=(lambdaD)/d`
Hence the fringe width is given by `beta = (lambdaD)/d`
APPEARS IN
RELATED QUESTIONS
In Young's double slit experiment, plot a graph showing the variation of fringe width versus the distance of the screen from the plane of the slits keeping other parameters same. What information can one obtain from the slope of the curve?
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
In Young’s double slit experiment, what is the effect on fringe pattern if the slits are brought closer to each other?
In Young’s double slit experiment, what should be the phase difference between the two overlapping waves to obtain 5th dark band/fringe on the screen?
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
In a double-slit experiment with monochromatic light, fringes are obtained on a screen placed at some distance from the plane of slits. If the screen is moved by 5 × 10-2 m towards the slits, the change in fringe width is 3 × 10-3 cm. If the distance between the slits is 1 mm, then the wavelength of the light will be ______ nm.
In Young's double slit experiment, the distance of the 4th bright fringe from the centre of the interference pattern is 1.5 mm. The distance between the slits and the screen is 1.5 m, and the wavelength of light used is 500 nm. Calculate the distance between the two slits.
