Advertisements
Advertisements
Question
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
Solution
Given:-
The thickness of the thin paper,
\[t = 0 . 02 mm = 0 . 02 \times {10}^{- 3} m\]
Refractive index of the paper,
\[\mu = 1 . 45\]
Wavelength of the light,
\[\lambda = 600 nm = 600 \times {10}^{- 9} m\]
(a)
Let the intensity of the source without paper = I1
and intensity of source with paper =I2
Let a1 and a2 be corresponding amplitudes.
As per the question,
\[I_2 = \frac{4}{9} I_1\]
We know that
\[\frac{I_1}{I_2} = \frac{{a_1}^2}{{a_2}^2}............\left( \because I \propto a^2 \right)\]
\[ \Rightarrow \frac{a_1}{a_2} = \frac{3}{2}\]
Here, a is the amplitude.
We know that \[\frac{I_\max}{I_\min} = \frac{\left( a_1 + a_2 \right)^2}{\left( a_1 - a_2 \right)^2}. \]
\[ \Rightarrow \frac{I_\max}{I_\min} = \frac{\left( 3 + 2 \right)^2}{\left( 3 - 2 \right)^2}\]
\[= \frac{25}{1}\]
\[ \Rightarrow I_\max : I_\min = 25 : 1\]
(b)
Number of fringes that will cross through the centre is given by \[n = \frac{\left( \mu - 1 \right)t}{\lambda}\]
\[\Rightarrow n = \frac{\left( 1 . 45 - 1 \right) \times 0 . 02 \times {10}^{- 3}}{600 \times {10}^{- 9}}\]
\[= \frac{0 . 45 \times 0 . 02 \times {10}^4}{6} = 15\]
APPEARS IN
RELATED QUESTIONS
In young’s double slit experiment, deduce the conditions for obtaining constructive and destructive interference fringes. Hence, deduce the expression for the fringe width.
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
Find the intensity at a point on a screen in Young's double slit experiment where the interfering waves have a path difference of (i) λ/6, and (ii) λ/2.
Write two characteristics features distinguish the diffractions pattern from the interference fringes obtained in Young’s double slit experiment.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
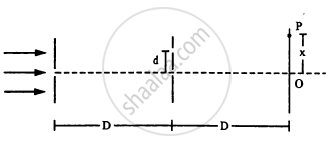
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
In Young’s double-slit experiment, using monochromatic light, fringes are obtained on a screen placed at some distance from the slits. If the screen is moved by 5 x 10-2 m towards the slits, the change in the fringe width is 3 x 10-5 m. If the distance between the two slits is 10-3 m, calculate the wavelength of the light used.
In Young’s double-slit experiment, show that:
`beta = (lambda "D")/"d"` where the terms have their usual meaning.
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
Answer the following question.
Write the conditions on path difference under which (i) constructive (ii) destructive interference occur in Young's double-slit experiment.
When a beam of light is used to determine the position of an object, the maximum accuracy is achieved, if the light is ______.
The force required to double the length of a steel wire of area 1 cm2, if its Young's modulus Y= 2 × 1011/m2 is:
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
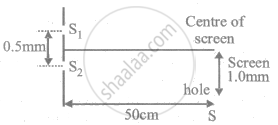
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
Two slits, 4mm apart, are illuminated by light of wavelength 6000 A° what will be the fringe width on a screen placed 2 m from the slits?
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
