Advertisements
Advertisements
Question
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
Solution
In Young's double-slit experiment, the separation between two slits is d.
Distance of the screen from the slit D = 1000 d
By using Bragg's law,
nλ = 2D sinθ
⇒ n = 1, D = 1000 d
⇒ 1 × λ = 2 × 1000 d sinθ
⇒ λ = 2000 d sinθ
d = `lambda/2000sintheta`
Hence, the relation between d and λ is `d = lambda/2000sintheta`.
APPEARS IN
RELATED QUESTIONS
In Young' s experiment the ratio of intensity at the maxima and minima . in the interference pattern is 36 : 16. What is the ratio of the widths of the two slits?
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
Young's double slit experiment is made in a liquid. The 10th bright fringe lies in liquid where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
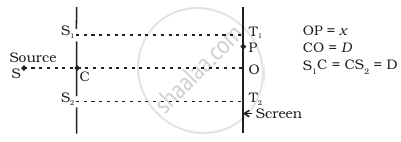
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100 cm. If a bright fringe is observed on a screen at distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this point from the slits is close to :
