Advertisements
Advertisements
Question
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
Options
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true and Reason (R) is NOT the correct explanation of Assertion (A).
Assertion (A) is true and Reason (R) is false.
Assertion (A) is false and Reason (R) is also false.
Solution
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Explanation:
Bright and dark fringes are produced as light travels through a slit in Young's double-slit experiment. Both the black and brilliant fringes are the same width as YDSE.
Statement 2 explanation: White light is used in Young's double-slit studies, and it is directed through the slit. Therefore, only brilliant and dark fringes may be seen utilising this source.
We know that fringe width is given by,
Width = `(lambdaD)/d`
Where,
λ = Wavelength of source used.
D = Distance between screen and slit.
d = Distance between slits.
As fringe width depends on all these factors so the fringe width remains constant.
APPEARS IN
RELATED QUESTIONS
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
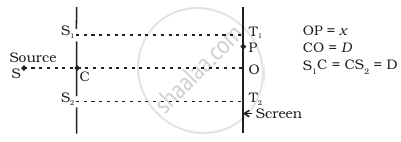
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the source slit is moved away from the plane of the slits?
Using Young’s double slit experiment, a monochromatic light of wavelength 5000Å produces fringes of fringe width 0.5 mm. If another monochromatic light of wavelength 6000Å is used and the separation between the slits is doubled, then the new fringe width will be ______.
