Advertisements
Advertisements
Questions
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is `λ /3`?
Advertisements
Solution 1
Phase difference = `(2pi)/lambda xx "Path difference"`
ϕ1 = `(2pi)/lambda xx lambda` = 2π
Where ϕ1 is the phase difference when the path difference is λ and the corresponding frequency is I1 = K
ϕ2 = `(2pi)/lambdaxxlambda/3=(2pi)/3`
Where ϕ2 is the phase difference when the path difference is the `lambda/3` and the corresponding frequency is I2.
Using equation, we get:
`I_1/I_2 = (4a^2cos^2(phi_1/2))/(4a^2cos^2(phi_2/2))`
`K/I_2 = (cos^2((2pi)/2))/cos^2(((2pi)/3)/2)`
`K/I_2 = (cos^2(pi))/cos^2(pi/3)`
`K/I_2 = 1/(1/(2^2))`
`K/I_2=4`
I2 = `K/4`
Solution 2
Let I1 and I2 be the intensity of the two light waves. Their resultant intensities can be obtained as:
I' = `I_1 + I_2 + 2sqrt(I_1 I_2) cos phi`
Where,
`phi` = Phase difference between the two waves
For monochromatic light waves,
I1 = I2
∴ I' = `I_1 + I_1 + 2sqrt(I_1I_1) cos phi`
= `2I_1 + 2I_1 cos phi`
Phase difference = `(2pi)/lambda xx "Path diffrence"`
Since path difference = λ,
Phase difference, `phi` = 2π
∴ I' = `2I_1 + 2I_1 = 4I_1`
Given
4I1 = K
∴ `I_1 = "K"/4` .....(1)
When path difference = `pi/3`
Phase difference, `phi = (2pi)/3`
Hence, resultant intensity, `I_R^' = I_1 + I_1 + 2sqrt(I_1I_1) cos (2pi)/3`
= `2I_1 + 2I_1(-1/2)`
= I1
Using equation (1), we can write:
IR = I1 = `K/4`
Hence, the intensity of light at a point where the path difference is `pi/3` is `K/4` units.
APPEARS IN
RELATED QUESTIONS
In a double-slit experiment using the light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
Show that the angular width of the first diffraction fringe is half that of the central fringe.
The fringes produced in diffraction pattern are of _______.
(A) equal width with same intensity
(B) unequal width with varying intensity
(C) equal intensity\
(D) equal width with varying intensity
If one of two identical slits producing interference in Young’s experiment is covered with glass, so that the light intensity passing through it is reduced to 50%, find the ratio of the maximum and minimum intensity of the fringe in the interference pattern.
Find the intensity at a point on a screen in Young's double slit experiment where the interfering waves have a path difference of (i) λ/6, and (ii) λ/2.
A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1 · 4 m away. If the two slits are separated by 0·28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
Can we perform Young's double slit experiment with sound waves? To get a reasonable "fringe pattern", what should be the order of separation between the slits? How can the bright fringes and the dark fringes be detected in this case?
A Young's double slit experiment is performed with white light.
(a) The central fringe will be white.
(b) There will not be a completely dark fringe.
(c) The fringe next to the central will be red.
(d) The fringe next to the central will be violet.
In a Young's double slit experiment, the separation between the slits = 2.0 mm, the wavelength of the light = 600 nm and the distance of the screen from the slits = 2.0 m. If the intensity at the centre of the central maximum is 0.20 W m−2, what will be the intensity at a point 0.5 cm away from this centre along the width of the fringes?
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
Draw the intensity distribution as function of phase angle when diffraction of light takes place through coherently illuminated single slit.
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
The Young's double slit experiment is performed with blue and with green light of wavelengths 4360Å and 5460Å respectively. If x is the distance of 4th maxima from the central one, then:
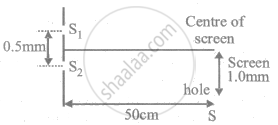
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
In a Young’s double slit experiment, the path difference at a certain point on the screen between two interfering waves is `1/8`th of the wavelength. The ratio of intensity at this point to that at the centre of a bright fringe is close to ______.
Two beams of light having intensities I and 41 interfere to produce a fringe pattern on a screen. The phase difference between the two beams are π/2 and π/3 at points A and B respectively. The difference between the resultant intensities at the two points is xl. The value of x will be ______.
In Young's double slit experiment the two slits are 0.6 mm distance apart. Interference pattern is observed on a screen at a distance 80 cm from the slits. The first dark fringe is observed on the screen directly opposite to one of the slits. The wavelength of light will be ______ nm.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
