Advertisements
Advertisements
प्रश्न
In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is `λ/3`.
In Young’s double-slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. What is the intensity of light at a point where path difference is `λ /3`?
Advertisements
उत्तर १
Phase difference = `(2pi)/lambda xx "Path difference"`
ϕ1 = `(2pi)/lambda xx lambda` = 2π
Where ϕ1 is the phase difference when the path difference is λ and the corresponding frequency is I1 = K
ϕ2 = `(2pi)/lambdaxxlambda/3=(2pi)/3`
Where ϕ2 is the phase difference when the path difference is the `lambda/3` and the corresponding frequency is I2.
Using equation, we get:
`I_1/I_2 = (4a^2cos^2(phi_1/2))/(4a^2cos^2(phi_2/2))`
`K/I_2 = (cos^2((2pi)/2))/cos^2(((2pi)/3)/2)`
`K/I_2 = (cos^2(pi))/cos^2(pi/3)`
`K/I_2 = 1/(1/(2^2))`
`K/I_2=4`
I2 = `K/4`
उत्तर २
Let I1 and I2 be the intensity of the two light waves. Their resultant intensities can be obtained as:
I' = `I_1 + I_2 + 2sqrt(I_1 I_2) cos phi`
Where,
`phi` = Phase difference between the two waves
For monochromatic light waves,
I1 = I2
∴ I' = `I_1 + I_1 + 2sqrt(I_1I_1) cos phi`
= `2I_1 + 2I_1 cos phi`
Phase difference = `(2pi)/lambda xx "Path diffrence"`
Since path difference = λ,
Phase difference, `phi` = 2π
∴ I' = `2I_1 + 2I_1 = 4I_1`
Given
4I1 = K
∴ `I_1 = "K"/4` .....(1)
When path difference = `pi/3`
Phase difference, `phi = (2pi)/3`
Hence, resultant intensity, `I_R^' = I_1 + I_1 + 2sqrt(I_1I_1) cos (2pi)/3`
= `2I_1 + 2I_1(-1/2)`
= I1
Using equation (1), we can write:
IR = I1 = `K/4`
Hence, the intensity of light at a point where the path difference is `pi/3` is `K/4` units.
APPEARS IN
संबंधित प्रश्न
A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in a Young’s double-slit experiment.
Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8th of the intensity of unpolarized light incident on A?
In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
A thin paper of thickness 0.02 mm having a refractive index 1.45 is pasted across one of the slits in a Young's double slit experiment. The paper transmits 4/9 of the light energy falling on it. (a) Find the ratio of the maximum intensity to the minimum intensity in the fringe pattern. (b) How many fringes will cross through the centre if an identical paper piece is pasted on the other slit also? The wavelength of the light used is 600 nm.
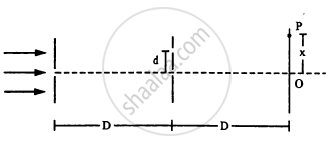
Consider the arrangement shown in the figure. The distance D is large compared to the separation d between the slits.
- Find the minimum value of d so that there is a dark fringe at O.
- Suppose d has this value. Find the distance x at which the next bright fringe is formed.
- Find the fringe-width.
In a Young's double slit interference experiment, the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength \[\lambda.\] Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one-fourth the maximum.
In Young's double slit experiment using monochromatic light of wavelength 600 nm, 5th bright fringe is at a distance of 0·48 mm from the centre of the pattern. If the screen is at a distance of 80 cm from the plane of the two slits, calculate:
(i) Distance between the two slits.
(ii) Fringe width, i.e. fringe separation.
"If the slits in Young's double slit experiment are identical, then intensity at any point on the screen may vary between zero and four times to the intensity due to single slit".
Justify the above statement through a relevant mathematical expression.
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
Two slits, 4mm apart, are illuminated by light of wavelength 6000 A° what will be the fringe width on a screen placed 2 m from the slits?
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
Why does the phase difference between light from ordinary sources change randomly?
What is the distance \\(x_n-x_m\\) between the \\(n\\)-th bright fringe and the \\(m\\)-th dark fringe?
What happens to fringe width when the wavelength of light increases while screen distance and slit separation remain unchanged?
